AI tutor
Full solution
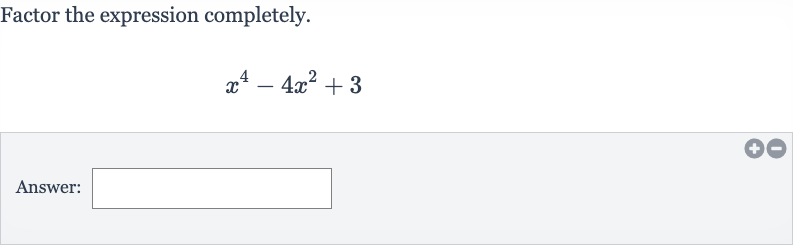
Q. Factor the expression completely.Answer:
- Identify Polynomial Type: Identify the type of polynomial and look for a factoring strategy.The given expression is a quadratic in form, but with a variable to the fourth power:This can be treated as a quadratic with taking the place of .
- Factor as Quadratic: Factor the expression as if it were a quadratic.We are looking for two binomials that multiply to give . The factors of that subtract to give are and .
- Check for Further Factoring: Check if the binomials can be factored further.The binomial is a difference of squares and can be factored further.The binomial cannot be factored further over the integers.
- Write Completely Factored Form: Write the completely factored form of the expression.The completely factored form of the expression is:
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help