Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Factor the expression completely.

-16x^(4)+40
Answer:

Factor the expression completely. $\newline$ $-16 x^{4}+40$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Solve exponential equations by rewriting the base

Full solution

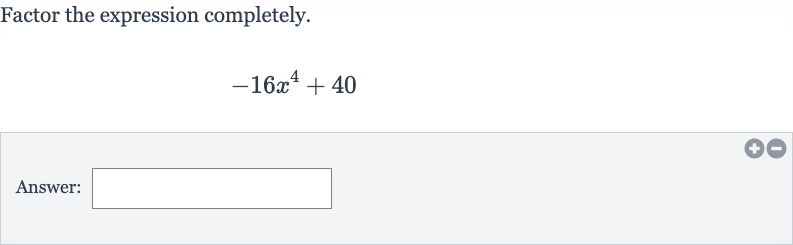
Q. Factor the expression completely.

\newline

-16 x^{4}+40

\newline

Answer:

Identify GCF: First, identify the greatest common factor (GCF) of the terms in the expression $-16x^{4}$ and $40$ . The GCF of $-16$ and $40$ is $8$ , and since there is no $x$ term in $40$ , $x$ cannot be part of the GCF. So, we factor out $-8$ from both terms.
Factor Out GCF: Now, write the expression as a product of the GCF and the remaining terms. $\newline$ $-16x^{4} + 40 = -8(2x^{4} - 5)$ $\newline$ Check to ensure that when you distribute $-8$ back into the parentheses, you get the original expression. $\newline$ $-8 \times 2x^{4} = -16x^{4}$ and $-8 \times (-5) = 40$ , which is correct.
Write as Product: Next, look inside the parentheses to see if the expression $2x^{4} - 5$ can be factored further. Since $2x^{4}$ is a term with an even power of $x$ and $5$ is a prime number, there are no common factors and it is not a difference of squares or any other factorable form. Therefore, the expression inside the parentheses cannot be factored further.
Check Distribution: The expression is now fully factored. $\newline$ The completely factored form of the expression $-16x^{4} + 40$ is $-8(2x^{4} - 5)$ .

More problems from Solve exponential equations by rewriting the base

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 3 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 3 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 2 months ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 3 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 3 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 2 months ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 3 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 3 months ago