AI tutor
Full solution
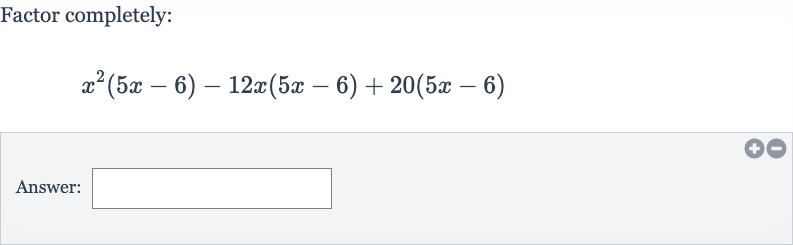
Q. Factor completely:Answer:
- Identify Common Factor: Identify the common factor in all terms.The common factor in all terms is .
- Factor Out Common Factor: Factor out the common factor . The expression becomes .
- Factor Quadratic Expression: Factor the quadratic expression.We need to factor . To do this, we look for two numbers that multiply to and add up to . These numbers are and .
- Write Factored Form: Write the factored form of the quadratic expression.The factored form of is .
- Combine Factored Expressions: Combine the factored quadratic with the common factor.The completely factored form of the original expression is .
More problems from Transformations of functions
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help