AI tutor
Full solution
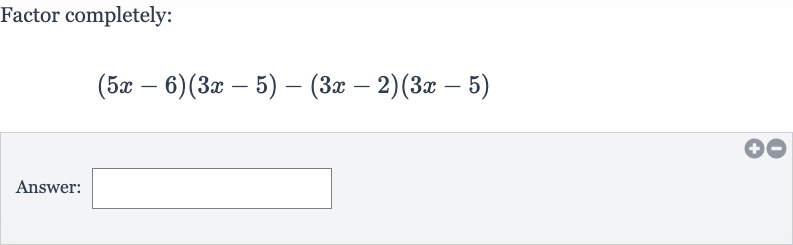
Q. Factor completely:Answer:
- Identify Common Factor: Identify the common factor in both terms.The common factor in both terms is .
- Factor Out Common Factor: Factor out the common factor .
- Simplify Inside Parentheses: Simplify the expression inside the parentheses.
- Combine Like Terms: Combine like terms.
- Write Factored Form: Write the factored form of the original expression.
- Check Further Factoring: Check if the expression can be factored further. can be factored as .
- Write Completely Factored Form: Write the completely factored form of the original expression.