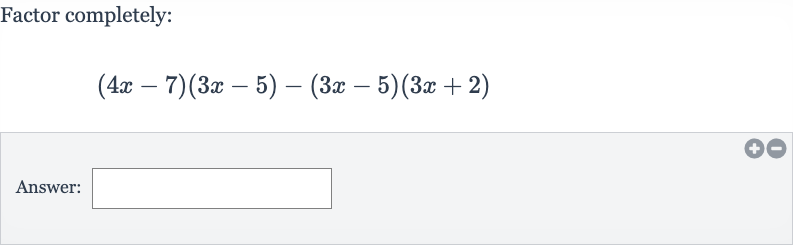AI tutor
Full solution
Q. Factor completely:Answer:
- Identify common factors: Identify common factors in both terms. We notice that is a common factor in both terms of the expression.
- Factor out common factor: Factor out the common factor .We can use the distributive property in reverse to factor out .
- Simplify expression inside brackets: Simplify the expression inside the brackets.Now we need to subtract the second term from the first term inside the brackets.
- Combine like terms: Combine like terms. Combine the terms and the constant terms.
- Write final factored form: Write the final factored form.Now that we have simplified the expression inside the brackets, we can write the final factored form.