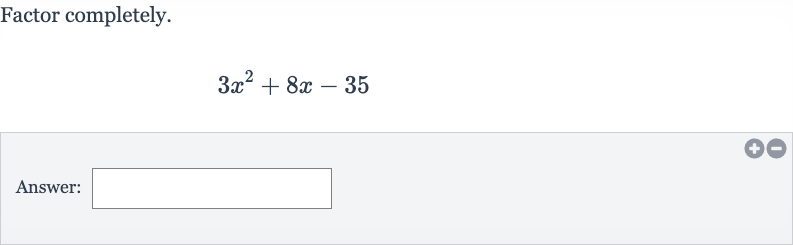
Factor completely. 3x^(2)+8x-35 Answer:

Question

Factor completely.  3x^(2)+8x-35 Answer:

Bytelearn · Accepted Answer

Identify the polynomial: Identify the polynomial to be factored. We are given the quadratic polynomial 3x^2 + 8x - 35, which is in the standard form ax^2 + bx + c, where a = 3, b = 8, and c = -35.Look for two numbers: Look for two numbers that multiply to ac (a times c) and add up to b. We need to find two numbers that multiply to (3)(-35) = -105 and add up to 8.Find the two numbers: Find the two numbers. After trying different combinations, we find that 15 and -7 multiply to -105 and add up to 8. 15 * -7 = -105 15 + (-7) = 8Rewrite the middle term: Rewrite the middle term using the two numbers found in Step 3. We can express 8x as 15x - 7x, which are the two numbers we found that add up to 8. 3x^2 + 8x - 35 = 3x^2 + 15x - 7x - 35Factor by grouping: Factor by grouping. Group the terms into two pairs and factor out the common factor from each pair. (3x^2 + 15x) + (-7x - 35) Factor out 3x from the first pair and -7 from the second pair. 3x(x + 5) - 7(x + 5)Factor out common binomial: Factor out the common binomial factor. The common binomial factor is (x + 5). Factor (x + 5) out of both terms. (3x - 7)(x + 5)

Factor completely. $\newline$ $3 x^{2}+8 x-35$ $\newline$ Answer:

Full solution

More problems from Add, subtract, multiply, and divide polynomials

Related topics

Factor completely.\newline3x2+8x−35 3 x^{2}+8 x-35 3x2+8x−35\newlineAnswer:

Factor completely. $\newline$ $3 x^{2}+8 x-35$ $\newline$ Answer: