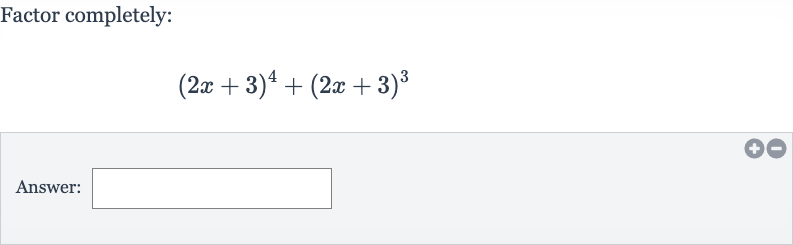Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Factor completely: (2x+3)^(4)+(2x+3)^(3) Answer:

Factor completely:\newline(2x+3)4+(2x+3)3 (2 x+3)^{4}+(2 x+3)^{3} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Transformations of functionsright chevron icon

Full solution

Q. Factor completely:\newline(2x+3)4+(2x+3)3 (2 x+3)^{4}+(2 x+3)^{3} \newlineAnswer:
  1. Recognize common factor: Recognize the common factor in both terms.\newlineBoth terms have a common factor of (2x+3)3(2x+3)^{3}. We can factor this out using the distributive property.
  2. Factor out common factor: Factor out the common factor of (2x+3)3(2x+3)^{3}.(2x+3)4+(2x+3)3=(2x+3)3×((2x+3)+1)(2x+3)^{4}+(2x+3)^{3} = (2x+3)^{3} \times ((2x+3) + 1)
  3. Simplify inside parentheses: Simplify the expression inside the parentheses.\newline(2x+3)+1=2x+3+1=2x+4(2x+3) + 1 = 2x + 3 + 1 = 2x + 4
  4. Write final factored form: Write the final factored form.\newlineThe factored expression is (2x+3)3×(2x+4)(2x+3)^{3} \times (2x + 4).

More problems from Transformations of functions

Question
Find g(x)g(x), where g(x)g(x) is the reflection across the x-axis of f(x)=9∣x+2∣−4f(x)=9|x+2|-4.\newlineChoices:\newline(A)g(x)=9∣x+2∣−4]\text{}(A)g(x) = 9|x+2| - 4\text{]}\newline(B)g(x)=9∣x−2∣−4]\text{}(B)g(x) = 9|x-2| - 4\text{]}\newline(C)g(x)=−9∣x−2∣+4]\text{}(C)g(x)=-9|x-2| +4\text{]}\newline(D)g(x)=−9∣x+2∣+4]\text{(D)}g(x) = -9|x + 2| + 4\text{]}
Get tutor helpright-arrow

Posted 9 months ago

Question
What does the transformation f(x)↦f(x−4) f(x) \mapsto f(x - 4) do to the graph of f(x) f(x) ?\newlineChoices:\newline(A) translates it 4 units right\text{translates it } 4 \text{ units right}\newline(B) translates it 4 units down\text{translates it } 4 \text{ units down}\newline(C) translates it 4 units left\text{translates it } 4 \text{ units left}\newline(D) translates it 4 units up\text{translates it } 4 \text{ units up}
Get tutor helpright-arrow

Posted 9 months ago

Question
What does the transformation f(x)↦f(4x) f(x) \mapsto f(4x) do to the graph of f(x) f(x) ?\newlineChoices:\newline[A] stretches it vertically\newline[B] stretches it horizontally\newline[C]shrinks it horizontally\newline[D]shrinks it vertically
Get tutor helpright-arrow

Posted 8 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 99 units down of f(x)=10x+8f(x) = 10x + 8.\newlineChoices:\newline(A) g(x)=10x−82g(x) = 10x - 82 \newline(B) g(x)=10x+98g(x) = 10x + 98 \newline(C) g(x)=10x−1g(x) = 10x - 1\newline(D) g(x)=10x+17g(x) = 10x + 17
Get tutor helpright-arrow

Posted 9 months ago

Question
What kind of transformation converts the graph of f(x)=−3x2−4 f(x) = -3x^2 - 4 into the graph of g(x)=−3x2+6 g(x) = -3x^2 + 6 ?\newlineChoices:\newline[A]translation 10 units up \text{[A]translation 10 units up} \newline[B]translation 10 units down \text{[B]translation 10 units down} \newline[C]translation 10 units left \text{[C]translation 10 units left} \newline[D]translation 10 units right \text{[D]translation 10 units right}
Get tutor helpright-arrow

Posted 8 months ago

Question
The parabola y=x2y=x^{2} is scaled vertically by a factor of 77. What is the equation of the new parabola?\newliney=y=
Get tutor helpright-arrow

Posted 10 months ago

Question
The parabola y=x2y=x^{2} is shifted down by 66 units and to the right by 55 units.\newlineWhat is the equation of the new parabola?\newliney=y=
Get tutor helpright-arrow

Posted 10 months ago

Question
The parabola y=x2y=x^{2} is shifted up by 22 units and to the right by 33 units.\newlineWhat is the equation of the new parabola?\newliney=y=
Get tutor helpright-arrow

Posted 8 months ago

Question
The parabola y=x2 y=x^{2} is reflected across the x x -axis and then scaled vertically by a factor of 55 .\newlineWhat is the equation of the new parabola?\newliney=□ y=\square
Get tutor helpright-arrow

Posted 8 months ago

Question
The parabola y=x2 y=x^{2} is scaled vertically by a factor of 110 \frac{1}{10} .\newlineWhat is the equation of the new parabola?\newliney= y=
Get tutor helpright-arrow

Posted 9 months ago

View all (82)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant