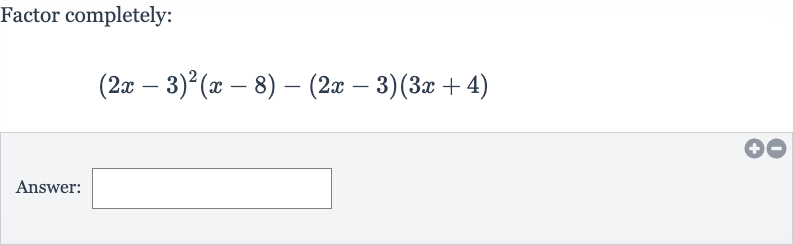Factor completely: (2x-3)^(2)(x-8)-(2x-3)(3x+4) Answer:

Question

Factor completely:  (2x-3)^(2)(x-8)-(2x-3)(3x+4) Answer:

Bytelearn · Accepted Answer

Identify Common Factor: Identify the common factor in both terms. The expression is (2x-3)^(2)(x-8)-(2x-3)(3x+4). We can see that (2x-3) is a common factor in both terms.Factor Out Common Factor: Factor out the common factor (2x-3). We can write the expression as (2x-3)[(2x-3)(x-8)-(3x+4)] by factoring out (2x-3).Distribute Common Factor: Distribute (2x-3) in the first term inside the brackets. Now we distribute (2x-3) to (x-8) to get (2x-3)[(2x-3)(x-8)] = (2x-3)(2x^2 - 16x + 3x - 24).Combine Like Terms: Combine like terms inside the brackets. Simplify the expression inside the brackets to get (2x-3)(2x^2 - 13x - 24).Subtract and Simplify: Subtract (3x+4) from the simplified expression inside the brackets. Now subtract (3x+4) from (2x^2 - 13x - 24) to get (2x-3)(2x^2 - 13x - 24 - 3x - 4).Combine Like Terms: Combine like terms inside the brackets after subtraction. Combine the terms to get (2x-3)(2x^2 - 16x - 28).Factor Quadratic Expression: Factor the quadratic expression inside the brackets if possible. We need to check if the quadratic expression 2x^2 - 16x - 28 can be factored further. However, this quadratic does not factor nicely with integer coefficients, so it is already in its simplest form.Write Final Factored Form: Write the final factored form. The completely factored form of the expression is (2x-3)(2x^2 - 16x - 28).

Factor completely: $\newline$ $(2 x-3)^{2}(x-8)-(2 x-3)(3 x+4)$ $\newline$ Answer:

Full solution

More problems from Add, subtract, multiply, and divide polynomials

Related topics

Factor completely:\newline(2x−3)2(x−8)−(2x−3)(3x+4) (2 x-3)^{2}(x-8)-(2 x-3)(3 x+4) (2x−3)2(x−8)−(2x−3)(3x+4)\newlineAnswer:

Factor completely: $\newline$ $(2 x-3)^{2}(x-8)-(2 x-3)(3 x+4)$ $\newline$ Answer: