Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Factor
64+125a^(3) completely.
Answer:

Factor $64+125 a^{3}$ completely. $\newline$ Answer:

View step-by-step help

View step-by-step help

Estimate positive square roots

Full solution

Q. Factor

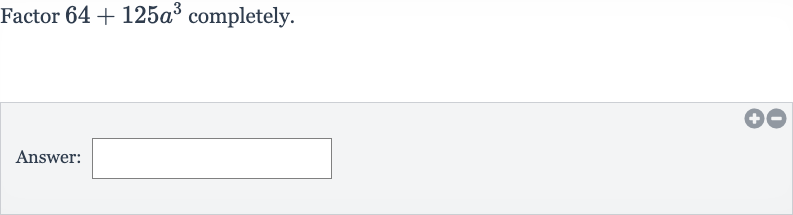
64+125 a^{3}

completely.

\newline

Answer:

Recognize as sum of cubes: Recognize the expression as a sum of two cubes. The given expression is $64 + 125a^{3}$ . We can rewrite $64$ as $(4)^{3}$ and $125a^{3}$ as $(5a)^{3}$ . This allows us to express the given sum as a sum of cubes: $(4)^{3} + (5a)^{3}$ .
Apply sum of cubes formula: Apply the sum of cubes formula. $\newline$ The sum of cubes formula is $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$ . We will apply this formula to our expression where $a = 4$ and $b = 5a$ .
Substitute values: Substitute the values into the sum of cubes formula. $\newline$ Using the values $a = 4$ and $b = 5a$ , we get the factorization $(4 + 5a)((4)^2 - (4)(5a) + (5a)^2)$ .
Simplify factors: Simplify the factors. $\newline$ Now we simplify each factor: $\newline$ First factor: $(4 + 5a)$ remains the same. $\newline$ Second factor: $(4)^2 - (4)(5a) + (5a)^2$ simplifies to $16 - 20a + 25a^2$ .
Write final factorization: Write the final factorization. $\newline$ The complete factorization of the expression is $(4 + 5a)(16 - 20a + 25a^2)$ .

More problems from Estimate positive square roots

Question

\sqrt{49}

?

\newline

Posted 1 month ago

Question

Complete the following statement. Use the integers that are closest to the number in the middle.

\newline

<

\sqrt{40}

<

Posted 1 month ago

Question

-\sqrt{64}

\newline

Posted 2 months ago

Question

\sqrt[3]{27}

Posted 1 month ago

Question

Which two integers is

-\sqrt{48}

\newline

\newline

[A]-6 \text{ and } -5

\newline

[B]5 \text{ and } 6

\newline

[C]-7 \text{ and } -6

\newline

[D]6 \text{ and } 7

Posted 6 days ago

Question

What is the cube root of

-64

\newline

Posted 2 months ago

Question

Which two integers is

\sqrt[3]{22}

\newline

\newline

[1 \text{ and } 2]

\newline

[15 \text{ and } 16]

\newline

[16 \text{ and } 17]

\newline

[2 \text{ and } 3]

Posted 2 months ago

Question

\newline

(\sqrt{25})^2 = \_\_\_\_\_

Posted 1 month ago

Question

Look at this equation:

\newline

c^3 = 27

\newline

\newline

c

, the cube root of

27

\newline

c =

\newline

Posted 2 months ago

Question

Write the sentence as an equation.

\newline

172

is equal to the quotient of

x

4

\newline

/

) if you want to use a division sign.

\newline

Posted 1 month ago