AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
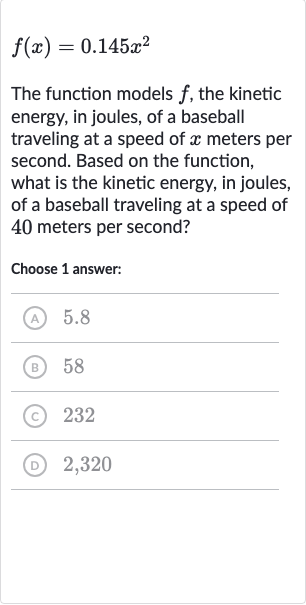
The function models , the kinetic energy, in joules, of a baseball traveling at a speed of meters per second. Based on the function, what is the kinetic energy, in joules, of a baseball traveling at a speed of meters per second?Choose answer:(A) .(B) (C) (D) ,
Full solution
Q. The function models , the kinetic energy, in joules, of a baseball traveling at a speed of meters per second. Based on the function, what is the kinetic energy, in joules, of a baseball traveling at a speed of meters per second?Choose answer:(A) .(B) (C) (D) ,
- Identify Function and Value: Identify the given function and the value to be substituted.The function given is , which models the kinetic energy of a baseball in joules based on its speed in meters per second. We need to find the kinetic energy when the speed is meters per second.
- Substitute Given Value: Substitute the given value into the function.We substitute into the function to calculate the kinetic energy.
- Perform Calculation: Perform the calculation.
- Multiply Coefficient: Multiply the coefficient by the square of the speed.
- Verify Result: Verify the result.The calculation seems correct, and the result is one of the given options, which suggests that no mathematical error has been made.
