Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Express the given expression without logs, in simplest form. Assume all variables represent positive values. (3^(log_(3)(7sqrtz))) Answer:

Express the given expression without logs, in simplest form. Assume all variables represent positive values.\newline(3log⁡3(7z)) \left(3^{\log _{3}(7 \sqrt{z})}\right) \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Properties of logarithms: mixed reviewright chevron icon

Full solution

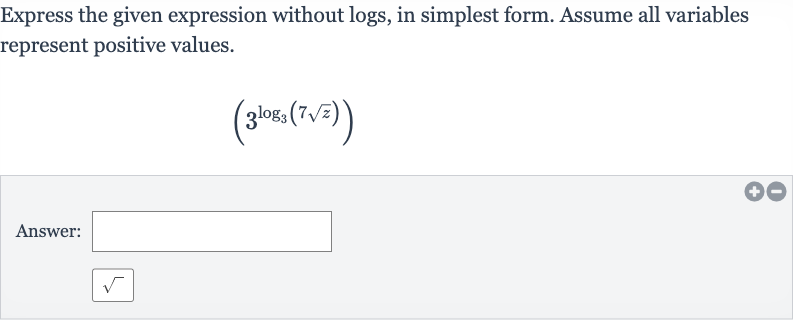
Q. Express the given expression without logs, in simplest form. Assume all variables represent positive values.\newline(3log⁡3(7z)) \left(3^{\log _{3}(7 \sqrt{z})}\right) \newlineAnswer:
  1. Recognize Property: Recognize the property of logarithms that will be used to simplify the expression.\newlineThe property that will be used is the inverse property of logarithms and exponents, which states that for any base bb, blog⁡b(x)=xb^{\log_b(x)} = x.
  2. Apply Inverse Property: Apply the inverse property of logarithms to the expression.\newlineUsing the inverse property, we can simplify 3log⁡3(7z)3^{\log_{3}(7\sqrt{z})} by recognizing that the base of the exponent and the base of the logarithm are the same (base 33).\newlineTherefore, 3log⁡3(7z)3^{\log_{3}(7\sqrt{z})} simplifies to 7z7\sqrt{z}.

More problems from Properties of logarithms: mixed review

Question
Write the exponential equation in logarithmic form.\newline93=7299^3 = 729\newlinelog⁡□729=3\log_\square 729 = 3
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the exponential equation in logarithmic form.\newlinee4≈54.598e^4 \approx 54.598\newlineln⁡____≈4\ln\_\_\_\_ \approx 4
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the logarithmic equation in exponential form.\newlinelog⁡10100=2\log_{10}100 = 2\newline102=‾10^2 = \underline{\hspace{2em}}
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.\newlineln⁡(e)10=\frac{\ln (e)}{10} = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Rewrite as a quotient of two common logarithms. Write your answer in simplest form.\newlinelog⁡333=\log_3 33 = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Round your answer to the nearest thousandth.\newlinelog⁡550=\log_{5}50 = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Which property of logarithms does this equation demonstrate? \newlinelog⁡33+log⁡36=log⁡318\log_3 3 + \log_3 6 = \log_3 18\newlineChoices:\newline(A) Product Property\text{Product Property}\newline(B) Power Property\text{Power Property}\newline(C) Quotient Property\text{Quotient Property}
Get tutor helpright-arrow

Posted 2 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡(uv)\log(uv)\newline_____
Get tutor helpright-arrow

Posted 2 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡v7\log v^7 \newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of base-66 logarithms or multiples of base-66 logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡6w6\log_6 w^6\newline______
Get tutor helpright-arrow

Posted 2 months ago

View all (5)