Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

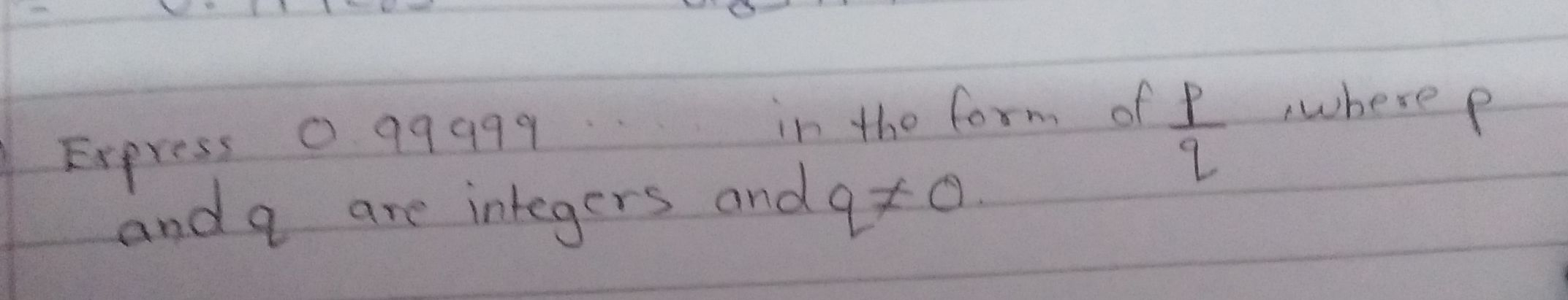
Express 0.99999 in the form of
(p)/(q) where
p and
q are integers and
q!=0.

Express $0$ . $99999$ in the form of $\frac{p}{q}$ where $p$ and $q$ are integers and $q \neq 0$ .

View step-by-step help

View step-by-step help

Transformations of linear functions

Full solution

Q. Express

0

.

99999

in the form of

\frac{p}{q}

where

p

and

q

are integers and

q \neq 0

.

Assign Variable $x$ : Let $x$ equal the repeating decimal we want to express as a fraction. $\newline$ Set $x = 0.99999$ .
Multiply by $10^5$ : Multiply both sides of the equation by $10^5$ ( $100000$ ) to shift the decimal point five places to the right, since there are five $9$ 's after the decimal. $\newline$ $100000x = 99999$ .
Subtract Original Equation: Subtract the original equation $x = 0.99999$ from the new equation $100000x = 99999$ to get rid of the repeating decimal. $\newline$ $100000x - x = 99999 - 0.99999$ .
Perform Subtraction: Perform the subtraction on both sides of the equation. $\newline$ $99999x = 99999 - 0.99999$ . $\newline$ $99999x = 99998.00001$ .
Solve for x: Solve for x by dividing both sides of the equation by $99999$ . $\newline$ x = rac{99998.00001}{99999}.
Simplify Numerator: Recognize that the subtraction in the numerator $99998.00001$ is very close to $99998$ , and the small difference is due to the repeating decimal. Since we are looking for a fraction with integers, we can simplify the numerator to $99998$ . $x = \frac{99998}{99999}$ .
Check Simplest Form: Check that the fraction is in simplest form. Since $99998$ and $99999$ have no common factors other than $1$ , the fraction is already in simplest form.

More problems from Transformations of linear functions

Question

This equation shows how the time required to screen-print a batch of shirts is related to the number of shirts in the batch.

\newline

t = s + 13

\newline

s

represents the number of shirts in the batch, and the variable

t

represents the time required to screen-print the shirts. How long does it take to screen-print a batch of

4

\newline

_________minutes

Posted 3 months ago

Question

Krysta wants to take piano lessons. She asked a teacher how many new pieces she could expect to learn each month. The teacher gave an estimate of

3

. Write an equation that shows how the total number of pieces Krysta would learn,

y

, depends on the number of months of piano lessons,

x

\newline

y

Posted 3 months ago

Question

Tom bought a boat for

\$3,000

and incurs a daily storage fee of

\$15

. Write a linear function to represent the total amount Tom will owe,

p(x)

x

days to pick it up.

\newline

Posted 4 months ago

Question

180

-page book cover to cover in a single session, at a constant rate. It took him

6

\newline

\newline

y

represent the number of pages left to read after

\newline

t

\newline

Which of the following information about the graph of the relationship is given?

\newline

1

\newline

\newline

x

\newline

\newline

y

\newline

(C) Slope and a point that is not an intercept

\newline

\newline

x

\newline

y

\newline

\newline

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Posted 4 months ago

Question

A charity organization had to sell

18

tickets to their fundraiser just to cover necessary production costs. They sold each ticket for

\$45

y

represent the net profit (in dollars) when they have sold

x

tickets. Which of the following information about the graph of the relationship is given?

\newline

1

\newline

x

\newline

y

\newline

(C) Slope and a point that is not an intercept

\newline

x

y

\newline

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Posted 2 months ago

Question

Hiro painted his room. After

3

hours of painting at a rate of

8

square meters per hour, he had

28

square meters left to paint.

\newline

\newline

y

represent the area (in square meters) left to paint after

\newline

x

\newline

Which of the following information about the graph of the relationship is given?

\newline

1

\newline

\newline

x

\newline

\newline

y

\newline

(C) Slope and a point that is not an intercept

\newline

\newline

x

\newline

y

\newline

\newline

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Posted 2 months ago

Question

Naoya read a book cover to cover in a single session, at a rate of

55

pages per hour. After

4

350

pages left to read.

\newline

y

represent the number of pages left to read after

x

\newline

Complete the equation for the relationship between the number of pages left and number of hours.

\newline

y=

Posted 1 month ago

Question

A teacher purchased

300

colored pencils for an upcoming project. The pencils she ordered come in packs of

20

30

14

packs in all. Write a system of equations to find the number of

20

(x)

30

(y)

the art teacher ordered.

Posted 2 months ago

Question

C=0.25(L-1200)

\newline

C

, in dollars, to the holder of a liability insurance account given a total liability of

L

dollars is given by the equation as long as

C

is positive. By how many dollars does the liability increase when the cost to the holder increases by

1

Posted 2 months ago

Question

P=\frac{2}{5} m+1.5

\newline

P

, in dollars, of a train ticket used to travel a distance of

m

miles is given by the equation. By how many miles does the traveling distance increase if the ticket price increases by

1

Posted 4 months ago