Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

P=(2)/(5)m+1.5
The price,
P, in dollars, of a train ticket used to travel a distance of
m miles is given by the equation. By how many miles does the traveling distance increase if the ticket price increases by 1 dollar?

$P=\frac{2}{5} m+1.5$ $\newline$ The price, $P$ , in dollars, of a train ticket used to travel a distance of $m$ miles is given by the equation. By how many miles does the traveling distance increase if the ticket price increases by $1$ dollar?

View step-by-step help

View step-by-step help

Write linear functions: word problems

Full solution

Q.

P=\frac{2}{5} m+1.5

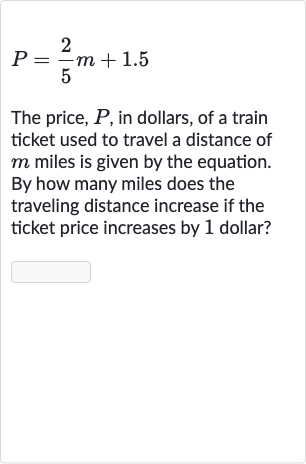
\newline

The price,

P

, in dollars, of a train ticket used to travel a distance of

m

miles is given by the equation. By how many miles does the traveling distance increase if the ticket price increases by

1

dollar?

Understand equation and question: Understand the given equation and what is asked. $\newline$ The equation $P = \frac{2}{5}m + 1.5$ represents the price of a train ticket in dollars for traveling a distance of $m$ miles. We need to find out how much the distance $m$ increases when the price $P$ increases by $1$ dollar.
Set up equation for price increase: Set up the equation to represent the increase in price. $\newline$ Let's say the initial price is $P$ dollars for $m$ miles. If the price increases by $1$ dollar, the new price will be $P + 1$ dollars for $m + \Delta m$ miles, where $\Delta m$ is the increase in distance we want to find.
Write equation for new price: Write the equation for the new price. $\newline$ Using the given equation, the new price $P + 1$ can be represented as: $\newline$ $P + 1 = \left(\frac{2}{5}\right)(m + \Delta m) + 1.5$
Substitute original price: Substitute the original price back into the equation. $\newline$ We know that the original price $P$ is $\frac{2}{5}m + 1.5$ , so we can substitute this back into the equation from Step $3$ to get: $\newline$ $\frac{2}{5}m + 1.5 + 1 = \frac{2}{5}(m + \Delta m) + 1.5$
Simplify the equation: Simplify the equation. $\newline$ Now we simplify the equation by subtracting $(\frac{2}{5})m + 1.5$ from both sides to isolate $\Delta m$ : $\newline$ $1 = (\frac{2}{5})\Delta m$
Solve for $\Delta m$ : Solve for $\Delta m$ .
To find $\Delta m$ , we divide both sides of the equation by $(2/5)$ :
$\Delta m = \frac{1}{(2/5)}$
$\Delta m = 1 \times \left(\frac{5}{2}\right)$
$\Delta m = \frac{5}{2}$
$\Delta m = 2.5$

More problems from Write linear functions: word problems

Question

This equation shows how the time required to screen-print a batch of shirts is related to the number of shirts in the batch.

\newline

t = s + 13

\newline

s

represents the number of shirts in the batch, and the variable

t

represents the time required to screen-print the shirts. How long does it take to screen-print a batch of

4

\newline

_________minutes

Posted 8 months ago

Question

Krysta wants to take piano lessons. She asked a teacher how many new pieces she could expect to learn each month. The teacher gave an estimate of

3

. Write an equation that shows how the total number of pieces Krysta would learn,

y

, depends on the number of months of piano lessons,

x

\newline

y

Posted 8 months ago

Question

Tom bought a boat for

\$3,000

and incurs a daily storage fee of

\$15

. Write a linear function to represent the total amount Tom will owe,

p(x)

x

days to pick it up.

\newline

Posted 9 months ago

Question

180

-page book cover to cover in a single session, at a constant rate. It took him

6

\newline

\newline

y

represent the number of pages left to read after

\newline

t

\newline

Which of the following information about the graph of the relationship is given?

\newline

1

\newline

\newline

x

\newline

\newline

y

\newline

(C) Slope and a point that is not an intercept

\newline

\newline

x

\newline

y

\newline

\newline

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Posted 10 months ago

Question

A charity organization had to sell

18

tickets to their fundraiser just to cover necessary production costs. They sold each ticket for

\$45

y

represent the net profit (in dollars) when they have sold

x

tickets. Which of the following information about the graph of the relationship is given?

\newline

1

\newline

x

\newline

y

\newline

(C) Slope and a point that is not an intercept

\newline

x

y

\newline

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Posted 8 months ago

Question

Hiro painted his room. After

3

hours of painting at a rate of

8

square meters per hour, he had

28

square meters left to paint.

\newline

\newline

y

represent the area (in square meters) left to paint after

\newline

x

\newline

Which of the following information about the graph of the relationship is given?

\newline

1

\newline

\newline

x

\newline

\newline

y

\newline

(C) Slope and a point that is not an intercept

\newline

\newline

x

\newline

y

\newline

\newline

y

-intercept and a point that is not an intercept

\newline

(F) Two points that are not intercepts

Posted 8 months ago

Question

Naoya read a book cover to cover in a single session, at a rate of

55

pages per hour. After

4

350

pages left to read.

\newline

y

represent the number of pages left to read after

x

\newline

Complete the equation for the relationship between the number of pages left and number of hours.

\newline

y=

Posted 7 months ago

Question

A teacher purchased

300

colored pencils for an upcoming project. The pencils she ordered come in packs of

20

30

14

packs in all. Write a system of equations to find the number of

20

(x)

30

(y)

the art teacher ordered.

Posted 8 months ago

Question

C=0.25(L-1200)

\newline

C

, in dollars, to the holder of a liability insurance account given a total liability of

L

dollars is given by the equation as long as

C

is positive. By how many dollars does the liability increase when the cost to the holder increases by

1

Posted 8 months ago

Question

You pick a card at random, put it back, and then pick another card at random.

\newline

4

\newline

5

\newline

6

\newline

7

\newline

What is the probability of picking a number greater than

5

and then picking a

4

\newline

Write your answer as a percentage.

Posted 1 month ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant