Expand the logarithm fully using the properties of logs. Express the final answer in terms of $\log x, \log y$ , and $\log z$ . $\newline$ $\log \frac{y x^{4}}{\sqrt[3]{z^{4}}}$ $\newline$ Answer:

View step-by-step help

Home

Math Problems

Precalculus

Quotient property of logarithms

Full solution

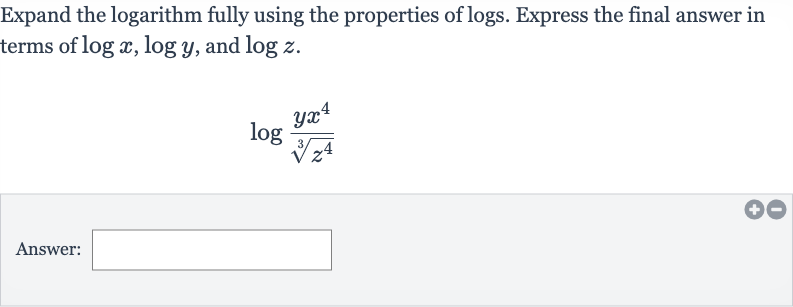
Q. Expand the logarithm fully using the properties of logs. Express the final answer in terms of

\log x, \log y

, and

\log z

\newline

\log \frac{y x^{4}}{\sqrt[3]{z^{4}}}

\newline

Answer:

Apply Quotient Rule: Apply the quotient rule of logarithms to the expression $\log\left(\frac{yx^{4}}{\sqrt[3]{z^{4}}}\right)$ . $\newline$ Quotient rule of logarithm: $\log\left(\frac{a}{b}\right) = \log(a) - \log(b)$ $\newline$ $\log\left(\frac{yx^{4}}{\sqrt[3]{z^{4}}}\right) = \log(yx^{4}) - \log(\sqrt[3]{z^{4}})$
Apply Product Rule: Apply the product rule of logarithms to the numerator $\log(yx^{4})$ . $\newline$ Product rule of logarithm: $\log(a \cdot b) = \log(a) + \log(b)$ $\newline$ $\log(yx^{4}) = \log(y) + \log(x^{4})$
Apply Power Rule: Apply the power rule of logarithms to $\log(x^{4})$ . $\newline$ Power rule of logarithm: $\log(a^{n}) = n \cdot \log(a)$ $\newline$ $\log(x^{4}) = 4 \cdot \log(x)$
Apply Power Rule: Apply the power rule of logarithms to the denominator $\log(\sqrt[3]{z^{4}})$ . The cube root can be written as a power of $\frac{1}{3}$ , and the power rule of logarithms can be applied. $\log(\sqrt[3]{z^{4}}) = \log((z^{4})^{\frac{1}{3}})$ $\log((z^{4})^{\frac{1}{3}}) = \frac{1}{3} \cdot \log(z^{4})$
Apply Power Rule: Apply the power rule of logarithms to $\log(z^{4})$ . $\newline$ $\log(z^{4}) = 4 \cdot \log(z)$
Substitute and Simplify: Substitute the results from Steps $3$ and $5$ into the expression from Step $1$ . $\log\left(\frac{y x^{4}}{\sqrt[3]{z^{4}}}\right) = (\log(y) + 4 \cdot \log(x)) - \left(\frac{1}{3}\right) \cdot (4 \cdot \log(z))$
Distribute and Simplify: Distribute the $\frac{1}{3}$ in the second term and simplify the expression. $\log\left(\frac{yx^{4}}{\sqrt[3]{z^{4}}}\right) = \log(y) + 4 \cdot \log(x) - \left(\frac{4}{3}\right) \cdot \log(z)$