Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of
log x,log y, and
log z.

log ((y^(2)root(3)(z^(2)))/(x^(5)))
Answer:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of $\log x, \log y$ , and $\log z$ . $\newline$ $\log \frac{y^{2} \sqrt[3]{z^{2}}}{x^{5}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Quotient property of logarithms

Full solution

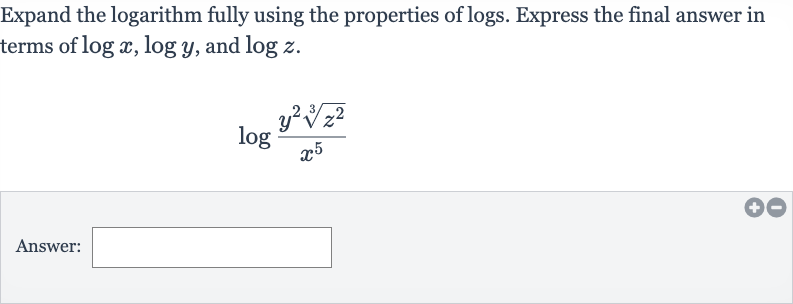
Q. Expand the logarithm fully using the properties of logs. Express the final answer in terms of

\log x, \log y

, and

\log z

.

\newline

\log \frac{y^{2} \sqrt[3]{z^{2}}}{x^{5}}

\newline

Answer:

Identify Properties: Identify the properties of logarithms that will be used to expand the given logarithm. $\newline$ The properties of logarithms that are relevant here are the quotient property, the power property, and the property for the logarithm of a root. $\newline$ Quotient Property: $\log_b(\frac{P}{Q}) = \log_b(P) - \log_b(Q)$ $\newline$ Power Property: $\log_b(P^k) = k \cdot \log_b(P)$ $\newline$ Root Property: $\log_b(\sqrt[k]{P}) = \frac{1}{k} \cdot \log_b(P)$
Apply Quotient Property: Apply the quotient property to the given logarithm. $\newline$ The given logarithm is of the form $\log\left(\frac{y^{2} \cdot \sqrt[3]{z^{2}}}{x^{5}}\right)$ . According to the quotient property, this can be written as: $\newline$ $\log(y^{2} \cdot \sqrt[3]{z^{2}}) - \log(x^{5})$
Apply Power Property: Apply the power property to the terms with exponents. $\newline$ The term $\log(y^{2})$ can be expanded using the power property as: $\newline$ $2 \times \log(y)$ $\newline$ Similarly, the term $\log(x^{5})$ can be expanded as: $\newline$ $5 \times \log(x)$
Apply Root Property: Apply the root property to the term with the cube root. $\newline$ The term $\sqrt[3]{z^{2}}$ can be written as $z^{\frac{2}{3}}$ , and applying the power property to $\log(z^{\frac{2}{3}})$ gives us: $\newline$ $\frac{2}{3} \cdot \log(z)$
Combine Results: Combine the results from the previous steps to write the final expanded form. $\newline$ The expanded form of the given logarithm is: $\newline$ $2 \cdot \log(y) + \frac{2}{3} \cdot \log(z) - 5 \cdot \log(x)$

More problems from Quotient property of logarithms

Question

Write the exponential equation in logarithmic form.

\newline

9^3 = 729

\newline

\log_\square 729 = 3

Posted 2 months ago

Question

Write the exponential equation in logarithmic form.

\newline

e^4 \approx 54.598

\newline

\ln\_\_\_\_ \approx 4

Posted 2 months ago

Question

Write the logarithmic equation in exponential form.

\newline

\log_{10}100 = 2

\newline

10^2 = \underline{\hspace{2em}}

Posted 2 months ago

Question

Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.

\newline

\frac{\ln (e)}{10} =

Posted 2 months ago

Question

Rewrite as a quotient of two common logarithms. Write your answer in simplest form.

\newline

\log_3 33 =

Posted 2 months ago

Question

Evaluate. Round your answer to the nearest thousandth.

\newline

\log_{5}50 =

Posted 2 months ago

Question

Which property of logarithms does this equation demonstrate?

\newline

\log_3 3 + \log_3 6 = \log_3 18

\newline

\newline

\text{Product Property}

\newline

\text{Power Property}

\newline

\text{Quotient Property}

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log(uv)

\newline

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log v^7

\newline

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of base-

6

logarithms or multiples of base-

6

logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log_6 w^6

\newline

Posted 2 months ago