Expand the logarithm fully using the properties of logs. Express the final answer in terms of $\log x, \log y$ , and $\log z$ . $\newline$ $\log \frac{\sqrt{y} z^{4}}{x^{2}}$ $\newline$ Answer:

View step-by-step help

Home

Math Problems

Precalculus

Quotient property of logarithms

Full solution

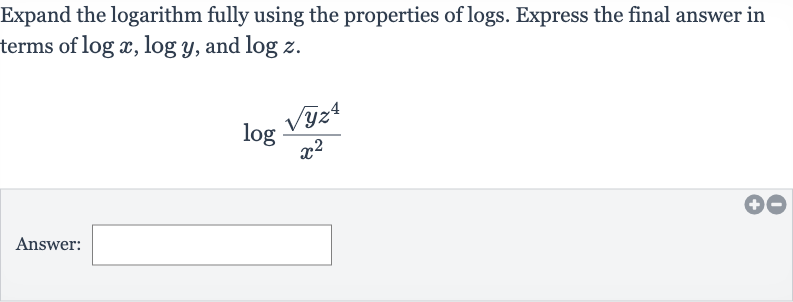
Q. Expand the logarithm fully using the properties of logs. Express the final answer in terms of

\log x, \log y

, and

\log z

\newline

\log \frac{\sqrt{y} z^{4}}{x^{2}}

\newline

Answer:

Apply Quotient Rule: Let's start by applying the quotient rule of logarithms, which states that $\log(\frac{a}{b}) = \log(a) - \log(b)$ . So, we have $\log\left(\frac{\sqrt{yz^{4}}}{x^{2}}\right) = \log(\sqrt{yz^{4}}) - \log(x^{2})$ .
Deal with First Term: Now, let's deal with the first term, $\log(\sqrt{yz^{4}})$ . The square root is the same as raising to the power of $\frac{1}{2}$ , so we can rewrite this as $\log((yz^{4})^{\frac{1}{2}})$ . $\newline$ Using the power rule of logarithms, which states that $\log(a^{n}) = n\log(a)$ , we get $\log((yz^{4})^{\frac{1}{2}}) = (\frac{1}{2})\log(yz^{4})$ .
Apply Product Rule: Next, we apply the product rule of logarithms to the term $\log(yz^{4})$ , which states that $\log(ab) = \log(a) + \log(b)$ . This gives us $(\frac{1}{2})\cdot(\log(y) + \log(z^{4}))$ .
Apply Power Rule: Now, let's apply the power rule again to $\log(z^{4})$ , which gives us $\log(z^{4}) = 4\log(z)$ . So, we have $(\frac{1}{2})\cdot(\log(y) + 4\log(z))$ .
Distribute Coefficients: We can distribute the $\frac{1}{2}$ to both terms inside the parenthesis, resulting in $(\frac{1}{2})\log(y) + (\frac{1}{2})\cdot 4\log(z)$ , which simplifies to $(\frac{1}{2})\log(y) + 2\log(z)$ .
Address Second Term: Now, let's address the second term from step $1$ , $\log(x^{2})$ . Applying the power rule of logarithms, we get $\log(x^{2}) = 2\cdot\log(x)$ .
Combine All Terms: Finally, we combine all the terms together to get the expanded form of the original logarithm. $\newline$ We have $\log(\sqrt{yz^{4}}) - \log(x^{2})$ which becomes $(\frac{1}{2})\log(y) + 2\log(z) - 2\log(x)$ .