Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of
log x,log y, and
log z.

log ((x)/(z^(5)y))
Answer:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of $\log x, \log y$ , and $\log z$ . $\newline$ $\log \frac{x}{z^{5} y}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Quotient property of logarithms

Full solution

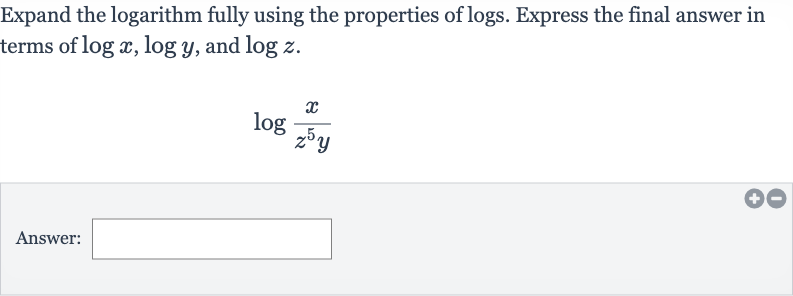
Q. Expand the logarithm fully using the properties of logs. Express the final answer in terms of

\log x, \log y

, and

\log z

.

\newline

\log \frac{x}{z^{5} y}

\newline

Answer:

Identify Properties: Identify the properties used to expand $\log\left(\frac{x}{z^{5}y}\right)$ . We will use the quotient property and the power property of logarithms to expand the given expression. Quotient Property: $\log_{b} \left(\frac{P}{Q}\right) = \log_{b} P - \log_{b} Q$ Power Property: $\log_{b} (P^{k}) = k \cdot \log_{b} P$
Apply Quotient Property: Apply the quotient property to $\log\left(\frac{x}{z^{5}y}\right)$ . Using the quotient property, we can separate the logarithm of the quotient into the difference of the logarithms of the numerator and the denominator. $\log\left(\frac{x}{z^{5}y}\right) = \log(x) - \log(z^{5}y)$
Apply Quotient Property Again: Apply the quotient property again to separate $\log(z^{5}y)$ . We can further expand $\log(z^{5}y)$ into $\log(z^{5}) + \log(y)$ using the product property of logarithms, which states that the logarithm of a product is the sum of the logarithms. $\log(z^{5}y) = \log(z^{5}) + \log(y)$
Apply Power Property: Apply the power property to $\log(z^{5})$ . Using the power property, we can take the exponent out in front of the logarithm. $\log(z^{5}) = 5 \cdot \log(z)$
Substitute Expanded Log: Substitute the expanded $\log(z^{5})$ back into the original expression. $\newline$ Now we replace $\log(z^{5})$ in our expression from Step $2$ with $5 \times \log(z)$ . $\newline$ $\log\left(\frac{x}{z^{5}y}\right) = \log(x) - (5 \times \log(z) + \log(y))$
Distribute Negative Sign: Distribute the negative sign to both terms in the parentheses. $\newline$ We need to apply the negative sign to both $\log(z^{5})$ and $\log(y)$ . $\newline$ $\log\left(\frac{x}{z^{5}y}\right) = \log(x) - 5 \cdot \log(z) - \log(y)$

More problems from Quotient property of logarithms

Question

Write the exponential equation in logarithmic form.

\newline

9^3 = 729

\newline

\log_\square 729 = 3

Posted 2 months ago

Question

Write the exponential equation in logarithmic form.

\newline

e^4 \approx 54.598

\newline

\ln\_\_\_\_ \approx 4

Posted 2 months ago

Question

Write the logarithmic equation in exponential form.

\newline

\log_{10}100 = 2

\newline

10^2 = \underline{\hspace{2em}}

Posted 2 months ago

Question

Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.

\newline

\frac{\ln (e)}{10} =

Posted 2 months ago

Question

Rewrite as a quotient of two common logarithms. Write your answer in simplest form.

\newline

\log_3 33 =

Posted 2 months ago

Question

Evaluate. Round your answer to the nearest thousandth.

\newline

\log_{5}50 =

Posted 2 months ago

Question

Which property of logarithms does this equation demonstrate?

\newline

\log_3 3 + \log_3 6 = \log_3 18

\newline

\newline

\text{Product Property}

\newline

\text{Power Property}

\newline

\text{Quotient Property}

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log(uv)

\newline

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log v^7

\newline

Posted 2 months ago

Question

Expand the logarithm. Assume all expressions exist and are well-defined.

\newline

Write your answer as a sum or difference of base-

6

logarithms or multiples of base-

6

logarithms. The inside of each logarithm must be a distinct constant or variable.

\newline

\log_6 w^6

\newline

Posted 2 months ago