Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of
log x, and
log y.

log x^(3)y
Answer:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of $\log x$ , and $\log y$ . $\newline$ $\log x^{3} y$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Power property of logarithms

Full solution

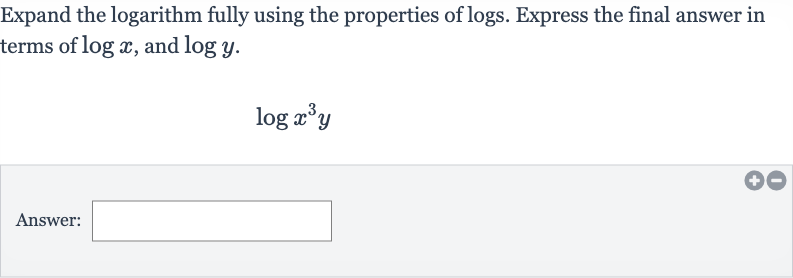
Q. Expand the logarithm fully using the properties of logs. Express the final answer in terms of

\log x

, and

\log y

.

\newline

\log x^{3} y

\newline

Answer:

Identify Properties: Identify the properties used to expand $\log x^{3}y$ . We will use the product property of logarithms to separate the terms, and the power property to bring down the exponent. Product property: $\log_b(mn) = \log_b(m) + \log_b(n)$ Power property: $\log_b(m^n) = n \cdot \log_b(m)$
Apply Product Property: Apply the product property to $\log x^{3}y$ . $\newline$ Product Property: $\log_b(mn) = \log_b(m) + \log_b(n)$ $\newline$ $\log x^{3}y = \log x^{3} + \log y$
Apply Power Property: Apply the power property to $\log x^{3}$ . $\newline$ Power Property: $\log_b(m^n) = n \cdot \log_b(m)$ $\newline$ $\log x^{3} = 3 \cdot \log x$
Combine Results: Combine the results from Step $2$ and Step $3$ . $\log x^{3}y = 3 \cdot \log x + \log y$

More problems from Power property of logarithms

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago