Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of log x,log y, and log z. log ((y^(5)x)/(root(3)(z^(4)))) Answer:

Expand the logarithm fully using the properties of logs. Express the final answer in terms of log⁡x,log⁡y \log x, \log y , and log⁡z \log z .\newlinelog⁡y5xz43 \log \frac{y^{5} x}{\sqrt[3]{z^{4}}} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Quotient property of logarithmsright chevron icon

Full solution

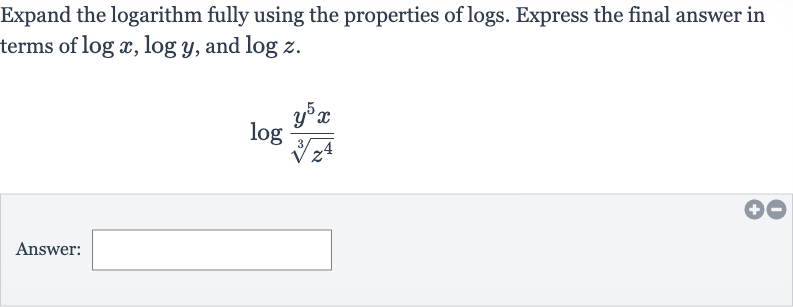
Q. Expand the logarithm fully using the properties of logs. Express the final answer in terms of log⁡x,log⁡y \log x, \log y , and log⁡z \log z .\newlinelog⁡y5xz43 \log \frac{y^{5} x}{\sqrt[3]{z^{4}}} \newlineAnswer:
  1. Identify Properties: Identify the properties used to expand the logarithm.\newlineWe will use the quotient property of logarithms to separate the numerator and denominator, the power property to bring down exponents, and the property for the logarithm of a product to separate the terms in the numerator.
  2. Apply Quotient Property: Apply the quotient property to the logarithm.\newlineThe quotient property states that log⁡b(PQ)=log⁡b(P)−log⁡b(Q)\log_b\left(\frac{P}{Q}\right) = \log_b(P) - \log_b(Q). We apply this to our logarithm:\newlinelog⁡(y5xz43)=log⁡(y5x)−log⁡(z43)\log\left(\frac{y^{5}x}{\sqrt[3]{z^{4}}}\right) = \log(y^{5}x) - \log(\sqrt[3]{z^{4}})
  3. Apply Product Property: Apply the product property to the logarithm of the numerator.\newlineThe product property states that log⁡b(PQ)=log⁡b(P)+log⁡b(Q)\log_b(PQ) = \log_b(P) + \log_b(Q). We apply this to the logarithm of the numerator:\newlinelog⁡(y5x)=log⁡(y5)+log⁡(x)\log(y^{5}x) = \log(y^{5}) + \log(x)
  4. Apply Power Property y5y^5: Apply the power property to the logarithm of y5y^5. The power property states that log⁡b(Pk)=k⋅log⁡b(P)\log_b(P^k) = k \cdot \log_b(P). We apply this to log⁡(y5)\log(y^{5}): \(\newline\log(y^{5}) = 5 \cdot \log(y)\)
  5. Apply Power Property z4z^4: Apply the power property to the logarithm of the denominator.\newlineWe need to express the cube root of z4z^4 as z43z^{\frac{4}{3}} and then apply the power property:\newlinelog⁡(z43)=log⁡(z43)=43⋅log⁡(z)\log(\sqrt[3]{z^{4}}) = \log(z^{\frac{4}{3}}) = \frac{4}{3} \cdot \log(z)
  6. Combine Properties: Combine all the properties to write the final expanded form.\newlineWe combine the results from steps 22 to 55 to get the final expanded form:\newlinelog⁡(y5xz43)=(log⁡(y5)+log⁡(x))−log⁡(z43)\log\left(\frac{y^{5}x}{\sqrt[3]{z^{4}}}\right) = (\log(y^{5}) + \log(x)) - \log(\sqrt[3]{z^{4}})\newline = (5⋅log⁡(y)+log⁡(x))−(43)⋅log⁡(z)(5 \cdot \log(y) + \log(x)) - \left(\frac{4}{3}\right) \cdot \log(z)\newline = 5⋅log⁡(y)+log⁡(x)−(43)⋅log⁡(z)5 \cdot \log(y) + \log(x) - \left(\frac{4}{3}\right) \cdot \log(z)

More problems from Quotient property of logarithms

Question
Write the exponential equation in logarithmic form.\newline93=7299^3 = 729\newlinelog⁡□729=3\log_\square 729 = 3
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the exponential equation in logarithmic form.\newlinee4≈54.598e^4 \approx 54.598\newlineln⁡____≈4\ln\_\_\_\_ \approx 4
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the logarithmic equation in exponential form.\newlinelog⁡10100=2\log_{10}100 = 2\newline102=‾10^2 = \underline{\hspace{2em}}
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.\newlineln⁡(e)10=\frac{\ln (e)}{10} = ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Rewrite as a quotient of two common logarithms. Write your answer in simplest form.\newlinelog⁡333=\log_3 33 = ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate. Round your answer to the nearest thousandth.\newlinelog⁡550=\log_{5}50 = ____
Get tutor helpright-arrow

Posted 3 months ago

Question
Which property of logarithms does this equation demonstrate? \newlinelog⁡33+log⁡36=log⁡318\log_3 3 + \log_3 6 = \log_3 18\newlineChoices:\newline(A) Product Property\text{Product Property}\newline(B) Power Property\text{Power Property}\newline(C) Quotient Property\text{Quotient Property}
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡(uv)\log(uv)\newline_____
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡v7\log v^7 \newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of base-66 logarithms or multiples of base-66 logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡6w6\log_6 w^6\newline______
Get tutor helpright-arrow

Posted 3 months ago

View all (63)