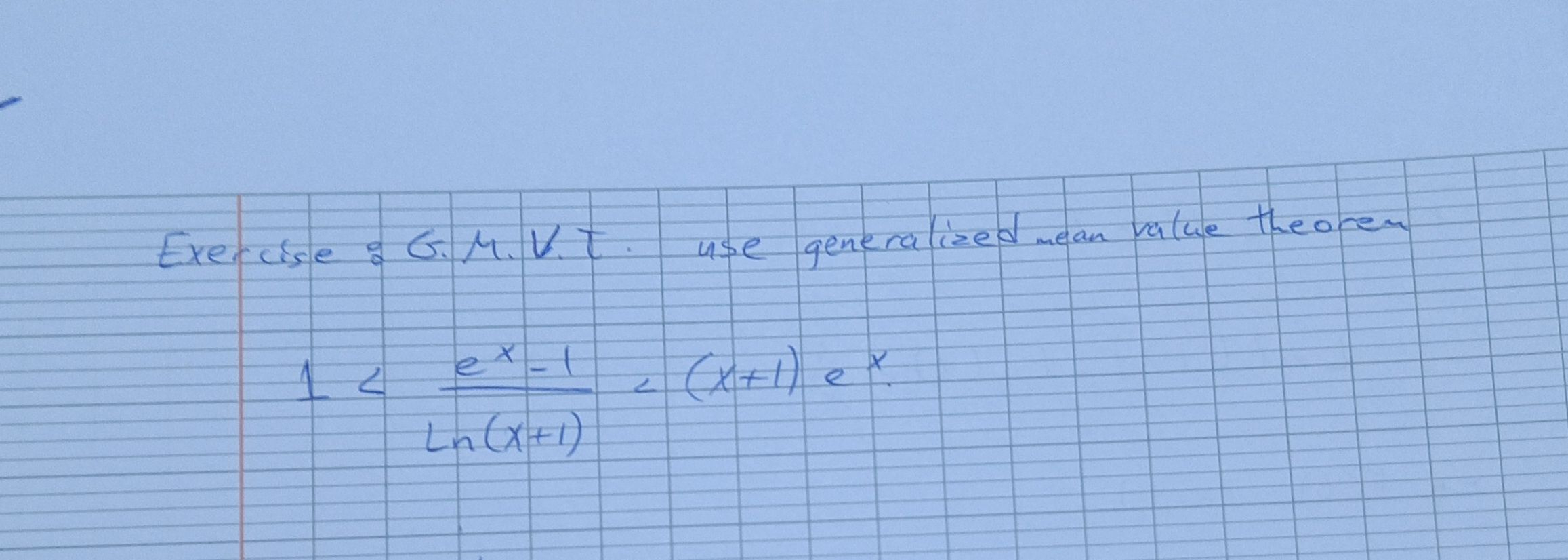
Exercise: G.M.V.T. use generalized mean value theorem $\newline$ $1<\frac{e^{x}-1}{\ln (x+1)}<(x+1) e^{x}$

View step-by-step help

Home

Math Problems

Algebra 2

Evaluate expression when two complex numbers are given

Full solution

Q. Exercise: G.M.V.T. use generalized mean value theorem

\newline

1<\frac{e^{x}-1}{\ln (x+1)}<(x+1) e^{x}

Understand GMVT: Let's first understand the Generalized Mean Value Theorem (GMVT). The GMVT states that if functions $f$ and $g$ are continuous on $[a, b]$ and differentiable on $(a, b)$ , then there exists some $c$ in $(a, b)$ such that $\frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f'(c)}{g'(c)}$ . We will apply this theorem to the functions $f(x) = e^x - 1$ and $g(x) = \ln(x + 1)$ on the interval $[0, x]$ for $g$ $0$ .
Check Functions: First, we need to check that $f(x) = e^x - 1$ and $g(x) = \ln(x + 1)$ are continuous on $[0, x]$ and differentiable on $(0, x)$ . The function $e^x$ is continuous and differentiable everywhere, and so is $e^x - 1$ . The function $\ln(x + 1)$ is continuous and differentiable for $x > -1$ , which includes our interval $[0, x]$ since $x > 0$ . Therefore, both $g(x) = \ln(x + 1)$ $0$ and $g(x) = \ln(x + 1)$ $1$ satisfy the conditions for the GMVT.
Find Derivatives: Now, we will find the derivatives of $f$ and $g$ . The derivative of $f(x) = e^x - 1$ is $f'(x) = e^x$ . The derivative of $g(x) = \ln(x + 1)$ is $g'(x) = \frac{1}{x + 1}$ .
Apply GMVT: Applying the GMVT, there exists some $c$ in $(0, x)$ such that $\frac{f(x) - f(0)}{g(x) - g(0)} = \frac{f'(c)}{g'(c)}$ . Substituting the functions and their derivatives, we get: $\newline$ $\frac{e^x - 1 - (e^0 - 1)}{\ln(x + 1) - \ln(0 + 1)} = \frac{e^c}{1 / (c + 1)}$ . $\newline$ Simplifying, we have: $\newline$ $\frac{e^x - 1}{\ln(x + 1)} = e^c \cdot (c + 1)$ .
Analyze Inequalities: Since $c$ is in $(0, x)$ , we know that $0 < c < x$ . Therefore, $e^c < e^x$ because the exponential function is increasing. Also, $c + 1 < x + 1$ for the same reason. Multiplying these two inequalities, we get $e^c \cdot (c + 1) < e^x \cdot (x + 1)$ .
Show Positivity: From the previous step, we have $(e^x - 1) / \ln(x + 1) = e^c * (c + 1)$ . Since $e^c * (c + 1) < e^x * (x + 1)$ , we can say that $(e^x - 1) / \ln(x + 1) < e^x * (x + 1)$ .
Consider Function $h(x)$ : Now we need to show that $1 < \frac{e^x - 1}{\ln(x + 1)}$ . We know that $e^x$ is always greater than $1$ for $x > 0$ , so $e^x - 1$ is positive. Since $\ln(x + 1)$ is also positive for $x > 0$ , the fraction $\frac{e^x - 1}{\ln(x + 1)}$ is positive. We need to show that it is greater than $1$ .
Use Derivative of $h(x)$ : Consider the function $h(x) = e^x - x - 1$ . Its derivative is $h'(x) = e^x - 1$ . Since $e^x > 1$ for $x > 0$ , $h'(x) > 0$ , which means $h(x)$ is increasing for $x > 0$ . Since $h(0) = 0$ , for $x > 0$ , we have $h(x) = e^x - x - 1$ $0$ , which means $h(x) = e^x - x - 1$ $1$ , or $h(x) = e^x - x - 1$ $2$ .
Combine Results: Since $e^x - 1 > x$ , we can divide both sides by $\ln(x + 1)$ (which is positive for $x > 0$ ) to get $(e^x - 1) / \ln(x + 1) > x / \ln(x + 1)$ . Since the function $x / \ln(x + 1)$ approaches $1$ as $x$ approaches $0$ from the right, and is increasing for $x > 0$ , we have $x / \ln(x + 1) > 1$ for $x > 0$ . Therefore, $\ln(x + 1)$ $1$ .
Combine Results: Since $e^x - 1 > x$ , we can divide both sides by $\ln(x + 1)$ (which is positive for $x > 0$ ) to get $(e^x - 1) / \ln(x + 1) > x / \ln(x + 1)$ . Since the function $x / \ln(x + 1)$ approaches $1$ as $x$ approaches $0$ from the right, and is increasing for $x > 0$ , we have $x / \ln(x + 1) > 1$ for $x > 0$ . Therefore, $\ln(x + 1)$ $1$ . Combining the results from the previous steps, we have shown that $\ln(x + 1)$ $2$ for $x > 0$ , which is what we wanted to prove using the Generalized Mean Value Theorem.