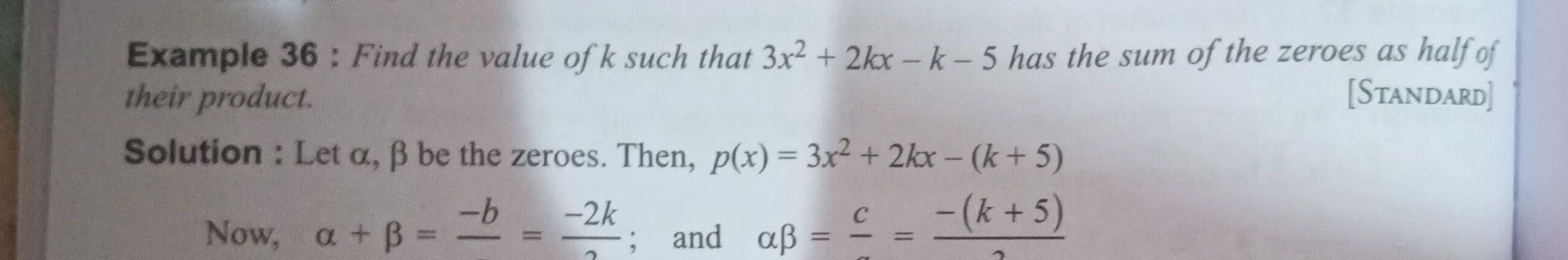Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the value of k such that 3x^(2)+2kx-k-5 has the sum of the zeroes as half of their product.

Find the value of $k$ such that $3 x^{2}+2 k x-k-5$ has the sum of the zeroes as half of their product.

View step-by-step help

View step-by-step help

Conjugate root theorems

Full solution

Q. Find the value of

k

such that

3 x^{2}+2 k x-k-5

has the sum of the zeroes as half of their product.

Denote the zeroes: Let's denote the zeroes of the polynomial by $\alpha$ (alpha) and $\beta$ (beta). According to Vieta's formulas, for a quadratic polynomial $ax^2 + bx + c$ , the sum of the roots is $-\frac{b}{a}$ and the product of the roots is $\frac{c}{a}$ . In our case, the polynomial is $3x^2 + 2kx - (k + 5)$ , so $a = 3$ , $b = 2k$ , and $c = -(k + 5)$ .
Find sum of roots: First, we find the sum of the roots using Vieta's formula: $\alpha + \beta = -\frac{b}{a} = -\frac{2k}{3}$ .
Find product of roots: Next, we find the product of the roots using Vieta's formula: $\alpha\beta = \frac{c}{a} = -\frac{(k + 5)}{3}$ .
Use given relation: The problem states that the sum of the zeroes is half of their product. This gives us the equation: $\alpha + \beta = \frac{1}{2} \times \alpha\beta$ . Substituting the expressions we found for the sum and product of the roots, we get: $-\frac{2k}{3} = \frac{1}{2} \times \left(-\frac{k + 5}{3}\right)$ .
Solve for k: Now, we solve for $k$ . Multiplying both sides by $3$ to eliminate the denominator, we get: $-2k = \frac{1}{2} \times -(k + 5)$ . Then, multiplying both sides by $2$ to get rid of the fraction, we have: $-4k = -(k + 5)$ .
Final value of k: Simplifying the equation, we add $k$ to both sides to get: $-3k = -5$ . Then, we divide both sides by $-3$ to solve for $k$ : $k = \frac{-5}{-3}$ .
Final value of k: Simplifying the equation, we add $k$ to both sides to get: $-3k = -5$ . Then, we divide both sides by $-3$ to solve for $k$ : $k = -5 / -3$ .Finally, we simplify the fraction to get the value of $k$ : $k = 5/3$ .

More problems from Conjugate root theorems

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 2 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 1 month ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 2 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 2 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 2 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 2 months ago