Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the logarithm. Round your answer to the nearest thousandth. log_(8)(5)~~

Evaluate the logarithm.\newlineRound your answer to the nearest thousandth.\newlinelog⁡8(5)≈ \log _{8}(5) \approx

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Compare linear, exponential, and quadratic growthright chevron icon

Full solution

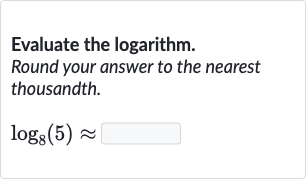
Q. Evaluate the logarithm.\newlineRound your answer to the nearest thousandth.\newlinelog⁡8(5)≈ \log _{8}(5) \approx
  1. Understand the problem: Understand the problem.\newlineWe need to evaluate the logarithm of 55 with base 88, which is written as log⁡8(5)\log_8(5). This means we are looking for the power to which we must raise 88 to get 55.
  2. Use the change of base formula: Use the change of base formula.\newlineThe change of base formula allows us to write log⁡8(5)\log_8(5) in terms of a logarithm with a more common base, such as 1010 or ee (natural logarithm). We will use base 1010 for this calculation.\newlineThe change of base formula is:\newlinelog⁡8(5)=log⁡10(5)log⁡10(8)\log_8(5) = \frac{\log_{10}(5)}{\log_{10}(8)}
  3. Calculate the logarithms: Calculate the logarithms using a calculator.\newlineUsing a calculator, we find:\newlinelog⁡10(5)≈0.69897\log_{10}(5) \approx 0.69897\newlinelog⁡10(8)≈0.90309\log_{10}(8) \approx 0.90309
  4. Divide the two logarithms: Divide the two logarithms.\newlineNow we divide the values we obtained in the previous step:\newlinelog⁡8(5)≈0.698970.90309\log_8(5) \approx \frac{0.69897}{0.90309}
  5. Perform the division: Perform the division to find the value of log⁡8(5)\log_8(5).0.698970.90309≈0.774\frac{0.69897}{0.90309} \approx 0.774
  6. Round the answer: Round the answer to the nearest thousandth.\newlineThe value we obtained in Step 55 is already rounded to the nearest thousandth, so our final answer is:\newlinelog⁡8(5)≈0.774\log_8(5) \approx 0.774

More problems from Compare linear, exponential, and quadratic growth

Question
We want to factor the following expression:\newlinex4+10x+25 x^{4}+10 x+25 \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to factor the following expression:\newline(x−2)4−(y+3)4 (x-2)^{4}-(y+3)^{4} \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to factor the following expression:\newline(x−1)2+(x−1)+4 (x-1)^{2}+(x-1)+4 \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to factor the following expression:\newline9x4+4y2 9 x^{4}+4 y^{2} \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to factor the following expression:\newline16x4−25 16 x^{4}-25 \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to factor the following expression:\newlinex4+3x2y+9y2 x^{4}+3 x^{2} y+9 y^{2} \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to factor the following expression:\newline(x+5)4+2(x+5)2−1 (x+5)^{4}+2(x+5)^{2}-1 \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to factor the following expression:\newline(x−3)2−10(x−3)+25 (x-3)^{2}-10(x-3)+25 \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to factor the following expression:\newline(x+7)2+2y(x+7)+y2 (x+7)^{2}+2 y(x+7)+y^{2} \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to factor the following expression:\newline9x6+6x3y+y2 9 x^{6}+6 x^{3} y+y^{2} \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 10 months ago

View all (23)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant