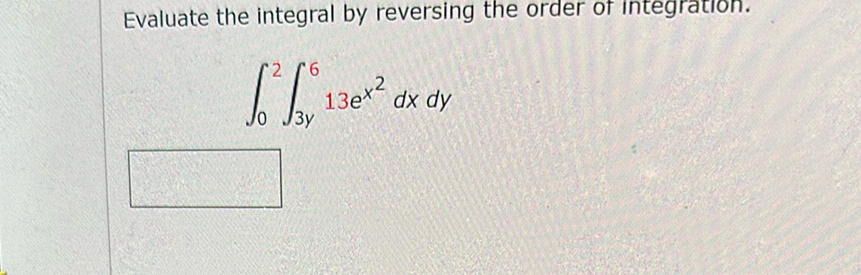Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral by reversing the order of integration. int_(0)^(2)int_(3y)^(6)13e^(x^(2))dxdy

Evaluate the integral by reversing the order of integration.\newline∫02∫3y613ex2dxdy \int_{0}^{2} \int_{3 y}^{6} 13 e^{x^{2}} d x d y

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Double integration by reversing the orderright chevron icon

Full solution

Q. Evaluate the integral by reversing the order of integration.\newline∫02∫3y613ex2dxdy \int_{0}^{2} \int_{3 y}^{6} 13 e^{x^{2}} d x d y
  1. Calculate Total Tape Needed: First, we need to determine the total amount of electrical tape the electrician needs and the amount of tape on each roll. We are given:\newlineTotal amount of electrical tape needed: 8,000 cm8,000\,\text{cm}\newlineAmount of tape on each roll: 2,000 cm2,000\,\text{cm}\newlineTo find out how many rolls the electrician should order, we divide the total amount of tape needed by the amount of tape on each roll.
  2. Divide to Find Rolls: Perform the division to calculate the number of rolls needed: 8,000 cm÷2,000 cm/roll=4 rolls8,000\,\text{cm} \div 2,000\,\text{cm}/\text{roll} = 4\,\text{rolls}
  3. Order Exact Amount: Since the result of the division is a whole number, the electrician should order exactly 44 rolls of tape to have the 8,0008,000 cm of electrical tape required for the job.

More problems from Double integration by reversing the order

Question
Evaluate the integral by reversing the order of integration.\newline∫03π∫y3πcos⁡(3x2)dxdy \int_{0}^{\sqrt{3} \pi} \int_{y}^{\sqrt{3 \pi}} \cos \left(3 x^{2}\right) d x d y
Get tutor helpright-arrow

Posted 11 months ago

Question
Evaluate the integral by reversing the order of integration,\newline∫02∫3y613ex2dxdy \int_{0}^{2} \int_{3 y}^{6} 13 e^{x^{2}} d x d y
Get tutor helpright-arrow

Posted 11 months ago

Question
Set up iterated integrals for both orders of integration. Then evaluate the double integral using the easier order. ∬DydA,D \iint_{D} y d A, \quad D is boundad by y=x−20,x=y2 y=x-20, x=y^{2}
Get tutor helpright-arrow

Posted 11 months ago

Question
Express 3−553+25 \frac{3-5 \sqrt{5}}{3+2 \sqrt{5}} in the form (a5−b) (a \sqrt{5}-b) where a a and b b are simple fractions.
Get tutor helpright-arrow

Posted 1 year ago

Question
let g(u,v,w)=uevw+veuw+weuvu2+v2+w2g(u,v,w)=\frac{u e^{v w}+v e^{u w}+w e^{u v}}{u^{2}+v^{2}+w^{2}}. calculate: g(1,2,3)g(1,2,3), g(3,2,1)g(3,2,1). do not simplify the exponent.
Get tutor helpright-arrow

Posted 11 months ago

Question
You pick a card at random, put it back, and then pick another card at random.\newline44\newline55\newline66\newline77\newlineWhat is the probability of picking a number greater than 55 and then picking a 44 ?\newlineWrite your answer as a percentage.
Get tutor helpright-arrow

Posted 6 months ago

Question
Jeanne's bank account earns interest annually. The equation shows her starting balance of $500\$500 and her balance at the end of three years, $546.36\$546.36. At what rate rr did Jeanne earn interest?\newline546.36=500(1+r)546.36 = 500(1 + r)
Get tutor helpright-arrow

Posted 6 months ago

Question
Jeanne's bank account earns interest annually. The equation shows her starting balance of $350 \$ 350 and her balance at the end of three years, $422.78 \$ 422.78 . At what rate r did Jeanne earn interest?\newline422.78=350(1+r)3422.78=350(1+r)^{3}
Get tutor helpright-arrow

Posted 6 months ago

Question
A leaky 10-kg10\text{-kg} bucket is lifted from the ground to a height of 14 m14\, \text{m} at a constant speed with a rope that weighs 0.6 kg/m0.6\, \text{kg/m}. Initially the bucket contains 42 kg42\, \text{kg} of water, but the water leaks at a constant rate and finishes draining just as the bucket reaches the 14 m14\, \text{m} level. How much work is done? (Use 9.8 m/s29.8\, \text{m/s}^2 for gg.) Show how to approximate the required work (in J\text{J}) by a Riemann sum. (Let xx be the height in meters above the ground. Enter xi∗x_i^* as xix_i.)
Get tutor helpright-arrow

Posted 6 months ago

Question
A leaky 10−kg 10-\mathrm{kg} bucket is lifted from the ground to a height of 1414 m at a constant speed with a rope that weighs 0.6 kg/m 0.6 \mathrm{~kg} / \mathrm{m} . Initially the bucket contains 4242 kg of water, but the water leaks at a constant rate and finishes draining just as the bucket reaches the 14−m 14-\mathrm{m} level. How much work is done? (Use 9.8 m/s2 9.8 \mathrm{~m} / \mathrm{s}^{2} for g .)\newlineShow how to approximate the required work (in J) by a Riemann sum. (Let x x be the height in meters above the ground. Enter xi∗∗ x_{i}^{* *} as xi x_{i} )\newlinelim⁡n→∞∑i=1n(98+35.28xi)Δx\lim _{n \rightarrow \infty} \sum_{i=1}^{n}\left(\boxed{98+35.28 x_{i}}\right) \Delta x\newlineExpress the work (in J) as an integral in terms of x x (in m).\newline∫014(98+35.28x\int_{0}^{14}(98+35.28 x\newlineEvaluate the integral (in J). (Round your answer to the nearest integer.)
Get tutor helpright-arrow

Posted 6 months ago

View all (6)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant