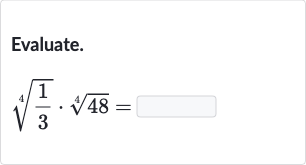Evaluate. root(4)((1)/(3))*root(4)(48)=

Question

Evaluate.  root(4)((1)/(3))*root(4)(48)=

Bytelearn · Accepted Answer

Understand the problem: Understand the problem. We need to find the product of the fourth roots of two numbers: (1/3) and 48. This means we will calculate the fourth root of each number and then multiply the results together.Calculate 1/3: Calculate the fourth root of 1/3. The fourth root of 1/3 is the number that, when raised to the power of 4, gives 1/3. Since 1 raised to any power is 1, the fourth root of 1/3 is simply the fourth root of 1 divided by the fourth root of 3.Calculate 48: Calculate the fourth root of 48. The fourth root of 48 is the number that, when raised to the power of 4, gives 48. We can simplify this by finding the prime factorization of 48 and then seeing if any groups of four identical factors emerge. 48 = 2 * 24 = 2 * 2 * 12 = 2 * 2 * 2 * 6 = 2 * 2 * 2 * 2 * 3 We have a group of four 2's, so the fourth root of 48 is 2 * the fourth root of 3.Multiply roots: Multiply the two fourth roots together. Now we multiply the fourth root of 1/3 from Step 2 with the fourth root of 48 from Step 3. (fourth root of 1/3) * (fourth root of 48) = (fourth root of 1 / fourth root of 3) * (2 * fourth root of 3)Simplify expression: Simplify the expression. We can see that the fourth root of 3 in the denominator and one in the numerator will cancel each other out, leaving us with: (fourth root of 1 / fourth root of 3) * (2 * fourth root of 3) = 2 * (fourth root of 1) Since the fourth root of 1 is 1, we are left with: 2 * 1 = 2

Evaluate. $\newline$ $\sqrt[4]{\frac{1}{3}} \cdot \sqrt[4]{48}=$

Full solution

More problems from Multiply two decimals: where does the decimal point go?

Related topics

Evaluate.\newline134⋅484= \sqrt[4]{\frac{1}{3}} \cdot \sqrt[4]{48}= 431​​⋅448​=

Evaluate. $\newline$ $\sqrt[4]{\frac{1}{3}} \cdot \sqrt[4]{48}=$