AI tutor
Full solution
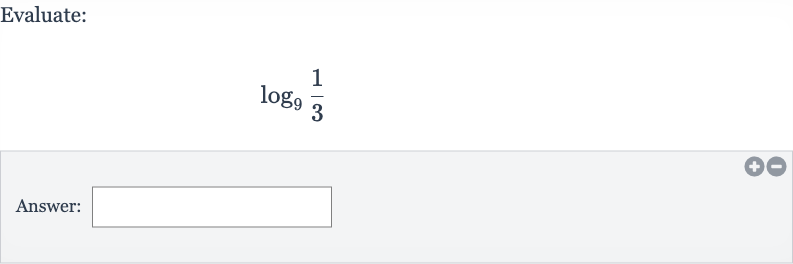
Q. Evaluate:Answer:
- Identify base and argument: Identify the base and the argument of the logarithm.We are given the logarithm . The base is , and the argument is .
- Use change of base: Use the change of base formula to rewrite the logarithm in terms of common logarithms.The change of base formula is , where is a new base we choose. We can choose base for common logarithms.
- Evaluate common logarithms: Evaluate the common logarithms.We know that is the logarithm of to the base , and is the logarithm of to the base . We can simplify these because is and is .
- Divide results: Divide the two results.Now we divide the two results from Step to find the value of the original logarithm.
- Simplify expression: Simplify the expression.Since appears in both the numerator and the denominator, they cancel each other out.