AI tutor
Full solution
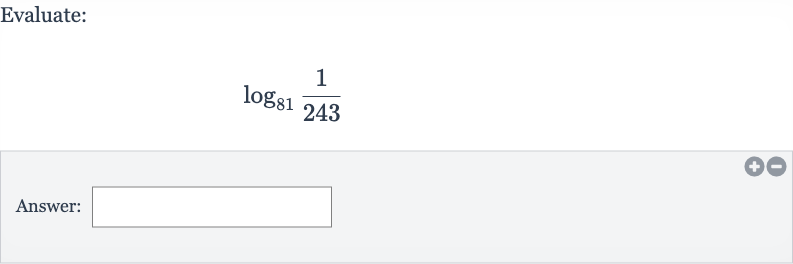
Q. Evaluate:Answer:
- Recognize Base and Argument: Recognize the base and the argument of the logarithm. We are given the logarithm . We need to evaluate this logarithm.
- Convert to Common Base: Convert the base and the argument into powers of a common base.Both and can be written as powers of , since and .
- Rewrite Using New Expressions: Rewrite the logarithm using the new expressions for the base and the argument. becomes .
- Apply Change of Base Formula: Apply the change of base formula for logarithms. The change of base formula is , where is a new base we choose. We can choose base for convenience. .
- Simplify Using Power Rule: Simplify the logarithms using the power rule.The power rule of logarithms states that . We apply this to both the numerator and the denominator..
- Evaluate Logarithms: Evaluate the logarithms.Since , we can simplify the expression further..