AI tutor
Full solution
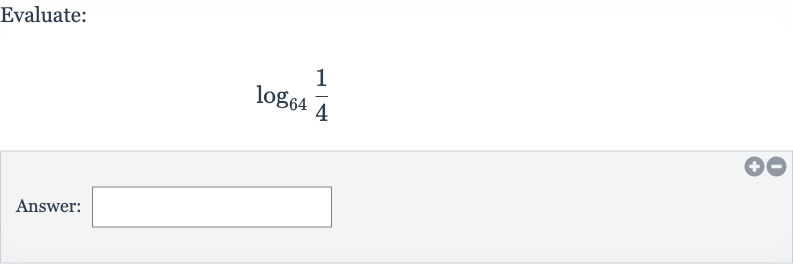
Q. Evaluate:Answer:
- Identify Properties: Identify the properties of logarithms that can be used to evaluate the expression.We have the logarithm . To evaluate this, we can use the change of base formula for logarithms, which states that for any positive base that is not equal to .
- Apply Change of Base: Apply the change of base formula to the given logarithm.Using the change of base formula with the common base of (since is a power of and so is ), we get:
- Evaluate Logarithms: Evaluate the logarithms using the known powers of .We know that and . Therefore, we can write: (since raised to the power of gives ) (since raised to the power of gives )
- Calculate Original Logarithm: Calculate the value of the original logarithm using the results from Step .Now we can divide the two logarithms we found:
- Simplify Fraction: Simplify the fraction to get the final answer.