AI tutor
Full solution
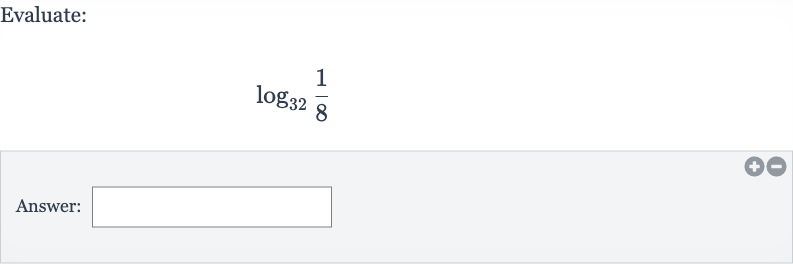
Q. Evaluate:Answer:
- Understand and Apply Change of Base Formula: Understand the problem and apply the change of base formula.We need to evaluate the logarithm of with base . The change of base formula states that , where is a new base we choose. A common choice for the new base is or , but in this case, we can choose to simplify the calculation since and are both powers of .
- Apply Change of Base with Base : Apply the change of base formula using base . Using base , we can rewrite the original logarithm as . We know that is and is .
- Evaluate Logarithms with Base : Evaluate the logarithms with base .Since and , we can substitute these values into our equation from Step . So, we have .
- Simplify the Fraction: Simplify the fraction.The fraction is already in its simplest form, so this is our final answer.