AI tutor
Full solution
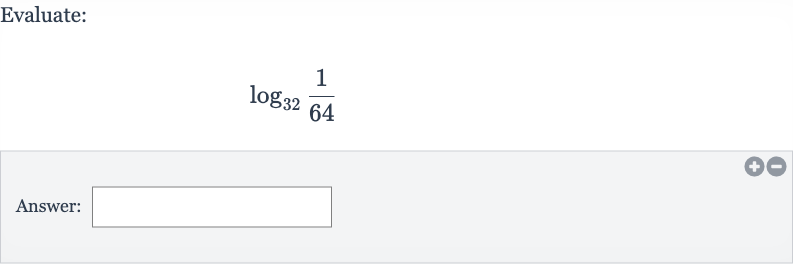
Q. Evaluate:Answer:
- Understand and Identify Properties: Understand the problem and identify the properties of logarithms to use.We need to evaluate the logarithm of with base . We can use the change of base formula for logarithms, which is , where all the logarithms are in the same base.
- Apply Change of Base Formula: Apply the change of base formula.Using the change of base formula, we can write the expression as:We will use the common logarithm (base ) for this calculation.
- Evaluate Using Known Values: Evaluate the logarithms using known values.We know that is and is . Therefore, we can rewrite the logarithms as:
- Divide Logarithms: Divide the two logarithms.Now we divide the two expressions we found in Step :Since is in both the numerator and the denominator, they cancel out, leaving us with: