AI tutor
Full solution
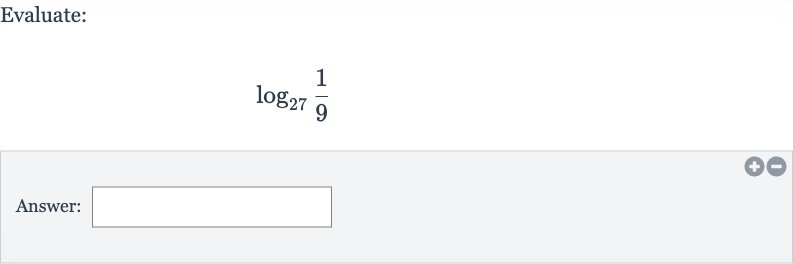
Q. Evaluate:Answer:
- Understand logarithm and base: Understand the logarithm and its base.We are given the logarithm . We need to evaluate this expression.
- Express in terms of base: Express in terms of the base . We know that is and is . Therefore, can be written as .
- Use change of base formula: Use the change of base formula.The change of base formula states that . We can use the base of for both the numerator and the denominator.
- Evaluate logarithms: Evaluate the logarithms.Since is , is . And since the base and the argument of the numerator are the same, is .So,
- Simplify expression: Simplify the expression.The expression simplifies to .