Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate:

log_(27)((1)/(243))
Answer:

Evaluate: $\newline$ $\log _{27} \frac{1}{243}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Evaluate logarithms

Full solution

Q. Evaluate:

\newline

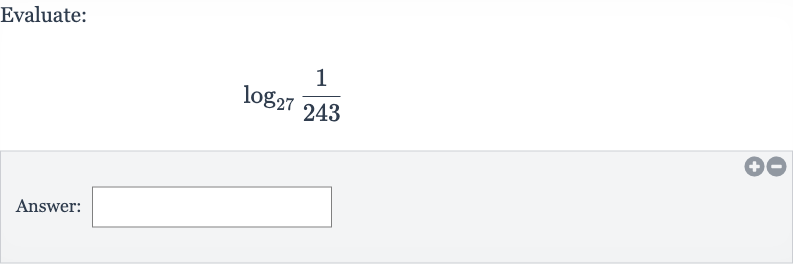
\log _{27} \frac{1}{243}

\newline

Answer:

Identify base and argument: Identify the base of the logarithm and the argument. $\newline$ The base of the logarithm is $27$ , and the argument is $(1)/(243)$ . $\newline$ We need to express both the base and the argument as powers of a common base to simplify the logarithm.
Express as powers of $3$ : Express the base $27$ and the argument $\frac{1}{243}$ as powers of $3$ . $\newline$ $27$ is a power of $3$ because $27 = 3^3$ . $\newline$ $243$ is also a power of $3$ because $243 = 3^5$ . $\newline$ Therefore, $27$ $0$ can be written as $27$ $1$ since $\frac{1}{243}$ is the reciprocal of $243$ .
Rewrite using new expressions: Rewrite the logarithm using the new expressions for the base and the argument. $\log_{27}\left(\frac{1}{243}\right)$ becomes $\log_{3^3}(3^{-5})$ .
Apply logarithm power rule: Apply the logarithm power rule. $\newline$ The power rule of logarithms states that $\log_b(a^n) = n \cdot \log_b(a)$ . $\newline$ Using this rule, we can simplify $\log_{3^3}(3^{-5})$ to $-5 \cdot \log_{3^3}(3)$ .
Evaluate $\log_{3^3}(3)$ : Evaluate the logarithm $\log_{3^3}(3)$ . Since the base of the logarithm $(3^3)$ and the argument $(3)$ are powers of the same number, we can simplify this further. $\log_{3^3}(3)$ is asking ＂ $3$ to what power gives $3$ ?＂ The answer is $1$ because $3^1 = 3$ . Therefore, $\log_{3^3}(3) = 1$ .
Multiply by $-5$ : Multiply the result from Step $5$ by $-5$ . $\newline$ $-5 \times \log_{3^3}(3) = -5 \times 1 = -5$ . $\newline$ This is the value of the original logarithm.

More problems from Evaluate logarithms

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago