Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate:

log_(25)125
Answer:

Evaluate: $\newline$ $\log _{25} 125$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Solve one-step multiplication and division equations with whole numbers

Full solution

Q. Evaluate:

\newline

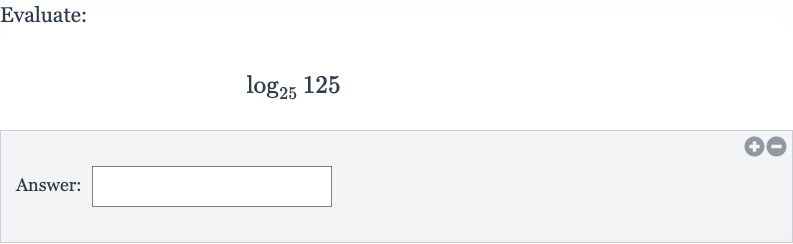
\log _{25} 125

\newline

Answer:

Determine Power of $25$ : To evaluate $\log_{25}125$ , we need to determine what power we must raise $25$ to in order to get $125$ . We can express $125$ as a power of $5$ , since $125$ is $5^3$ . Similarly, $25$ is $5^2$ . So, we can rewrite the expression as $\log_{5^2}(5^3)$ .
Express Numbers as Powers: Using the property of logarithms that $\log_{a^m}(b^n) = \frac{n}{m} \cdot \log_a(b)$ , we can simplify the expression. $\newline$ In this case, $\log_{5^2}(5^3) = \frac{3}{2} \cdot \log_5(5)$ .
Simplify Using Logarithm Property: We know that $\log_5(5)$ is $1$ , because $5$ raised to the power of $1$ is $5$ . So, $\frac{3}{2} \times \log_5(5) = \frac{3}{2} \times 1$ .
Calculate Logarithm Value: Multiplying $\frac{3}{2}$ by $1$ gives us $\frac{3}{2}$ . $\newline$ Therefore, $\log_{25}125 = \frac{3}{2}$ .

More problems from Solve one-step multiplication and division equations with whole numbers

Question

Write the sentence as an equation.

\newline

138

is equal to the quotient of

w

30

\newline

/

) if you want to use a division sign.

\newline

Posted 3 months ago

Question

\newline

(\frac{2}{7})x= -14

\newline

x =

Posted 4 months ago

Question

(\frac{8}{5})x= 32

Posted 4 months ago

Question

\newline

2+2

\newline

Posted 4 days ago

Question

-27x+18y=54

Posted 4 months ago

Question

\newline

48.5-0.434=

Posted 4 months ago

Question

\newline

96.7-0.163=

Posted 4 months ago

Question

\newline

4.43-0.283=

Posted 4 months ago

Question

\newline

3.05-0.338=

Posted 4 months ago

Question

\newline

6.168-0.432=

Posted 4 months ago