AI tutor
Full solution
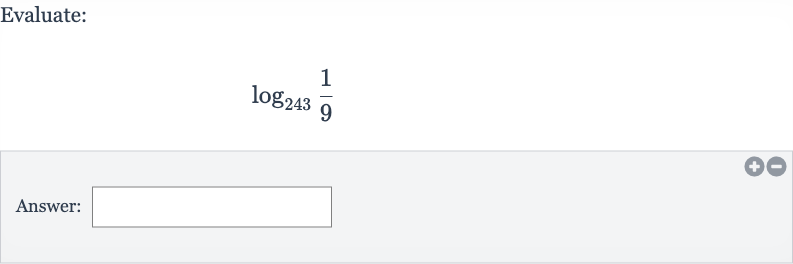
Q. Evaluate:Answer:
- Understand Problem and Identify Properties: Understand the problem and identify the properties of logarithms that can be used.We need to evaluate the logarithm of with base . We can use the change of base formula for logarithms, which states that can be written as , where is a new base we choose. In this case, we can choose base because and are both powers of .
- Express Powers of : Express and as powers of . is raised to the th power (), and is squared ().
- Apply Change of Base Formula: Apply the change of base formula using base . can be written as .
- Evaluate Logarithms Using Powers of : Evaluate the logarithms using the known powers of .
ext{log}_3 rac{1}{9} is the exponent we need to raise to get rac{1}{9}, which is because 3^{-2} = rac{1}{9}.
is the exponent we need to raise to get , which is because . - Calculate Logarithm Value: Calculate the value of the logarithm.Now we have which is .
- Simplify Fraction: Simplify the fraction. divided by is .