AI tutor
Full solution
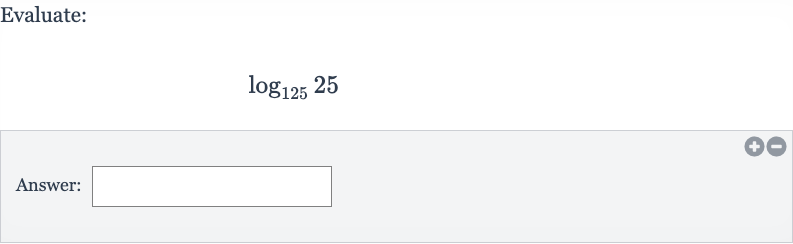
Q. Evaluate:Answer:
- Recognize Relationship: Recognize the relationship between the base of the logarithm and the number.The base of the logarithm is , and the number is . We know that is and is .
- Express as Power: Express the number as a power of the base .Since is , we can express as because .
- Apply Change of Base: Apply the change of base formula for logarithms.Using the change of base formula, we can write as .
- Simplify Using Power Rule: Simplify the logarithm using the power rule.The power rule of logarithms states that . Therefore, can be simplified to .
- Recognize Same Base: Recognize that the base and the number inside the logarithm are now the same. Since the base is and the number is , we can simplify to because is the cube root of .
- Multiply Final Result: Multiply the result from Step by the coefficient from Step .Multiplying by gives us the final result of the logarithm..