AI tutor
Full solution
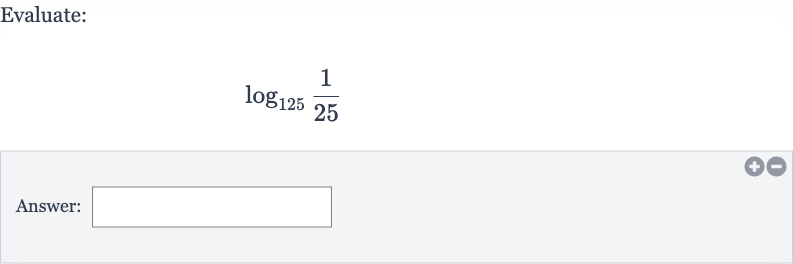
Q. Evaluate:Answer:
- Recognize base and argument: Recognize the base of the logarithm and the argument.We have . We can use the change of base formula to rewrite this logarithm in terms of common logarithms or natural logarithms.Change of base formula: , where is any positive number different from .
- Apply change of base formula: Apply the change of base formula using base , which is a common factor of both and .
- Evaluate with base : Evaluate both logarithms with base .Since is and is , we can rewrite the logarithms as: and
- Use power rule to simplify: Use the power rule of logarithms to simplify.The power rule states that .Therefore, and
- Further simplify: Since is equal to , we can further simplify. and
- Divide for final answer: Divide the results to get the final answer.