Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Determine the largest integer value of
x in the solution of the following inequality.

5x-3 <= -20
Answer:
x=

Determine the largest integer value of $x$ in the solution of the following inequality. $\newline$ $5 x-3 \leq-20$ $\newline$ Answer: $x=$

View step-by-step help

View step-by-step help

Solve logarithmic equations with multiple logarithms

Full solution

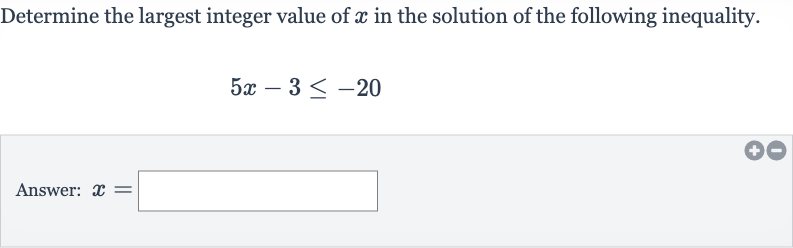
Q. Determine the largest integer value of

x

in the solution of the following inequality.

\newline

5 x-3 \leq-20

\newline

Answer:

x=

Add $3$ to isolate $x$ : Add $3$ to both sides of the inequality to isolate the term with $x$ on one side. $\newline$ $5x - 3 + 3 \leq -20 + 3$ $\newline$ $5x \leq -17$
Divide by $5$ : Divide both sides of the inequality by $5$ to solve for $x$ . $\frac{5x}{5} \leq \frac{-17}{5}$ $x \leq \frac{-17}{5}$
Consider integer part: Since we are looking for the largest integer value of $x$ , we need to consider the integer part of $-\frac{17}{5}$ . The integer part of $-\frac{17}{5}$ is $-4$ because $-3.4$ (which is $-\frac{17}{5}$ ) rounds down to $-4$ when looking for the largest integer less than or equal to $-3.4$ . $\newline$ $x \leq -4$

More problems from Solve logarithmic equations with multiple logarithms

Question

x

\newline

5^x=1

\newline

\newline

Write your answer in simplest form.

Posted 5 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

Posted 4 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

Posted 5 months ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 8 months ago

Question

x

\newline

7 = 9^x

\newline

Round your answer to the nearest thousandth.

Posted 4 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 7 months ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 9 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 7 months ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 4 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6x

\newline

f(x) = 6^x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 4 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant