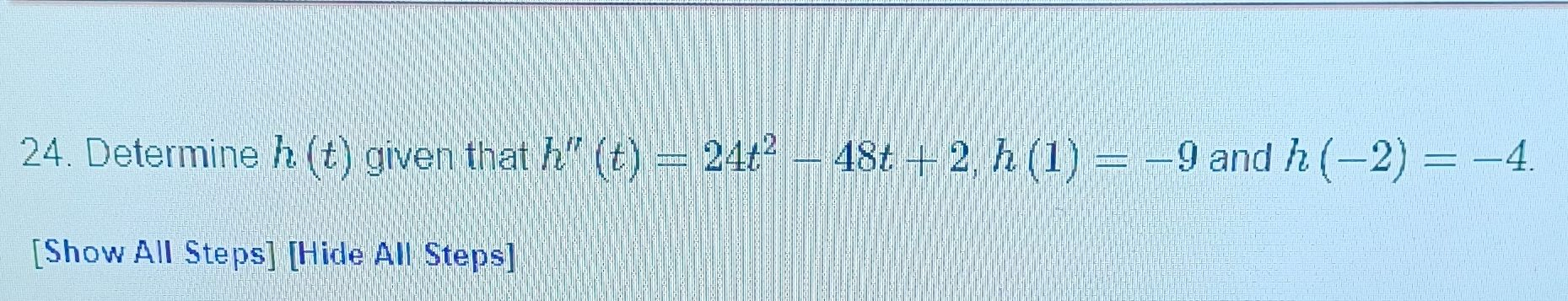Determine h(t) given that h^('')(t)=24t^(2)-48 t+2,h(1)=-9 and h(-2)=-4.

Question

Bytelearn · Accepted Answer

Integrate h''(t): To find h(t), we need to integrate h''(t) twice. The given second derivative is h''(t) = 24t^2 - 48t + 2. Let's integrate this to find the first derivative h'(t).Find h'(t): The integral of 24t^2 with respect to t is (24/3)t^3 = 8t^3. The integral of -48t with respect to t is (-48/2)t^2 = -24t^2. The integral of 2 with respect to t is 2t. We also add a constant of integration, C1. So, h'(t) = ∫(24t^2 - 48t + 2) dt = 8t^3 - 24t^2 + 2t + C1.Integrate h'(t) to find h(t): Now we integrate h'(t) to find h(t). The integral of 8t^3 with respect to t is (8/4)t^4 = 2t^4. The integral of -24t^2 with respect to t is (-24/3)t^3 = -8t^3. The integral of 2t with respect to t is (2/2)t^2 = t^2. We also add another constant of integration, C2. So, h(t) = ∫(8t^3 - 24t^2 + 2t + C1) dt = 2t^4 - 8t^3 + t^2 + C1t + C2.Use h(1) = -9: We have two initial conditions: h(1) = -9 and h(-2) = -4. We will use these to solve for the constants C1 and C2. First, let's use h(1) = -9. Plugging in t = 1, we get h(1) = 2(1)^4 - 8(1)^3 + (1)^2 + C1(1) + C2 = 2 - 8 + 1 + C1 + C2 = -5 + C1 + C2. Since h(1) = -9, we have -5 + C1 + C2 = -9.Use h(-2) = -4: Now let's use h(-2) = -4. Plugging in t = -2, we get h(-2) = 2(-2)^4 - 8(-2)^3 + (-2)^2 + C1(-2) + C2 = 32 + 64 + 4 - 2C1 + C2 = 100 - 2C1 + C2. Since h(-2) = -4, we have 100 - 2C1 + C2 = -4.Solve system of equations: We now have a system of two equations: 1) -5 + C1 + C2 = -9 2) 100 - 2C1 + C2 = -4 Let's solve this system for C1 and C2.Subtract equations to eliminate C2: Subtract equation 1) from equation 2) to eliminate C2: (100 - 2C1 + C2) - (-5 + C1 + C2) = -4 - (-9) 95 - 3C1 = 5 -3C1 = 5 - 95 -3C1 = -90 C1 = 30Find C1: Now that we have C1, we can substitute it back into equation 1) to find C2: -5 + 30 + C2 = -9 25 + C2 = -9 C2 = -9 - 25 C2 = -34Find C2: We have found C1 = 30 and C2 = -34. Now we can write the final form of h(t): h(t) = 2t^4 - 8t^3 + t^2 + 30t - 34.

Determine $h(t)$ given that $h^{\prime \prime}(t)=24 t^{2}-48 t+2, h(1)=-9$ and $h(-2)=-4$ .

Full solution

More problems from One-step inequalities: word problems

Related topics

Determine h(t) h(t) h(t) given that h′′(t)=24t2−48t+2,h(1)=−9 h^{\prime \prime}(t)=24 t^{2}-48 t+2, h(1)=-9 h′′(t)=24t2−48t+2,h(1)=−9 and h(−2)=−4 h(-2)=-4 h(−2)=−4.

Determine $h(t)$ given that $h^{\prime \prime}(t)=24 t^{2}-48 t+2, h(1)=-9$ and $h(-2)=-4$ .