Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

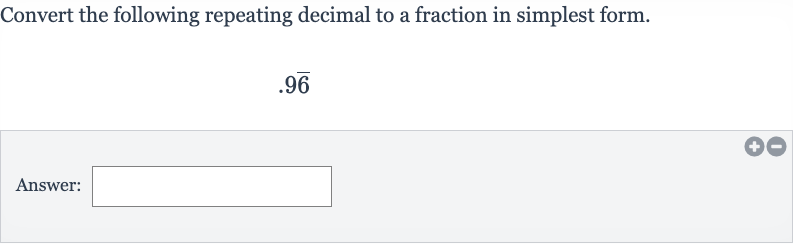
$Convert the following repeating decimal to a fraction in simplest form. .9 bar(6) Answer:$

Convert the following repeating decimal to a fraction in simplest form. $\newline$ $.9 \overline{6}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Divide decimals

Full solution

Q. Convert the following repeating decimal to a fraction in simplest form.

\newline

.9 \overline{6}

\newline

Answer:

Denote Repeating Decimal: Let's denote the repeating decimal $0.9$ with a repeating $6$ as $x$ . $\newline$ $x = 0.966666...$ $\newline$ To convert this repeating decimal to a fraction, we can use an algebraic method where we multiply $x$ by a power of $10$ to move the decimal point to the right of the repeating digits.
Multiply by $10$ : We multiply $x$ by $10$ to shift the decimal point one place to the right: $\newline$ $10x = 9.666666...$ $\newline$ Notice that the digits after the decimal point are the same as in $x$ , which is crucial for the next step.
Subtract to Eliminate Decimals: Now we set up an equation to subtract $x$ from $10x$ , which will eliminate the repeating decimals: $\newline$ $10x - x = 9.666666... - 0.966666...$ $\newline$ This subtraction will give us a whole number on the right side of the equation.
Solve for x: Performing the subtraction, we get: $\newline$ $9x = 8.7$ $\newline$ Now we have an equation without repeating decimals that we can solve for $x$ .
Divide by $9$ : To find $x$ , we divide both sides of the equation by $9$ : $\newline$ $x = \frac{8.7}{9}$
Convert to Fraction: Now we convert the decimal $8.7$ to a fraction. The decimal $8.7$ is the same as $\frac{87}{10}$ , so we substitute that into our equation: $\newline$ $x = \frac{\frac{87}{10}}{9}$
Simplify Fraction: To simplify the fraction, we multiply the denominator $10$ by $9$ : $x = \frac{87}{(10 \times 9)}$ $x = \frac{87}{90}$
Find GCD and Divide: We can simplify the fraction $\frac{87}{90}$ by finding the greatest common divisor (GCD) of $87$ and $90$ and dividing both the numerator and the denominator by the GCD. $\newline$ The GCD of $87$ and $90$ is $3$ .
Final Simplified Fraction: Divide both the numerator and the denominator by the GCD: $\newline$ $x = (87 \div 3) / (90 \div 3)$ $\newline$ $x = \frac{29}{30}$ $\newline$ This is the fraction in its simplest form.

More problems from Divide decimals

Question

Convert the following repeating decimal to a fraction in simplest form.

\newline

.6 \overline{8}

\newline

Posted 2 months ago

Question

Convert the following repeating decimal to a fraction in simplest form.

\newline

.9 \overline{4}

\newline

Posted 2 months ago

Question

Which expression is equivalent to

99.7-(-57.9)

\newline

99.7-57.9

\newline

57.9-99.7

\newline

-57.9-99.7

\newline

99.7+57.9

Posted 2 months ago

Question

Find the value of

x

in the equation below.

\newline

x-13.6=7.6

\newline

x=

Posted 2 months ago

Question

A scientist was in a submarine below sea level, studying ocean life. Over the next ten minutes, she dropped

68

1

feet. How many feet had she been below sea level, if she was

155

4

feet below sea level after she dropped?

\newline

\square

Posted 2 months ago

Question

A scientist was in a submarine below sea level, studying ocean life. Over the next ten minutes, she went down

36

3

feet. How many feet had she been below sea level, if she was

99

7

feet below sea level after she went down?

\newline

\square

Posted 2 months ago

Question

A scientist was in a submarine below sea level, studying ocean life. Over the next ten minutes, she descended

22

feet. How many feet had she been below sea level, if she was

52

3

feet below sea level after she descended?

\newline

\square

Posted 2 months ago

Question

A scientist was in a submarine below sea level, studying ocean life. Over the next ten minutes, she dropped

88

6

feet. How many feet had she been below sea level, if she was

182

5

feet below sea level after she dropped?

\newline

\square

Posted 2 months ago

Question

A scientist was in a submarine,

41

4

feet below sea level, studying ocean life. Over the next ten minutes, she rose

33

6

feet. How many feet was she now below sea level?

\newline

\square

Posted 2 months ago

Question

Plot the vertex. Then plot another point on the parabola. If you make a mistake, you can erase your parabola by selecting the second point and placing it on top of the first.

\newline

\newline

Posted 7 hours ago