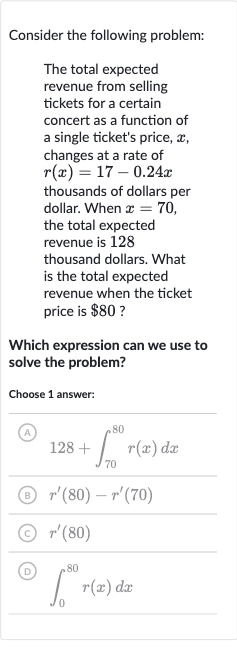
Consider the following problem: The total expected revenue from selling tickets for a certain concert as a function of a single ticket's price, x, changes at a rate of r(x)=17-0.24 x thousands of dollars per dollar. When x=70, the total expected revenue is 128 thousand dollars. What is the total expected revenue when the ticket price is $80 ? Which expression can we use to solve the problem? Choose 1 answer: (A) 128+int_(70)^(80)r(x)dx (B) r^(')(80)-r^(')(70) (C) r^(')(80) (D) int_(0)^(80)r(x)dx

Question

Consider the following problem: The total expected revenue from selling tickets for a certain concert as a function of a single ticket's price,  x, changes at a rate of  r(x)=17-0.24 x thousands of dollars per dollar. When  x=70, the total expected revenue is 128 thousand dollars. What is the total expected revenue when the ticket price is  $80 ? Which expression can we use to solve the problem? Choose 1 answer: (A)  128+int_(70)^(80)r(x)dx (B)  r^(')(80)-r^(')(70) (C)  r^(')(80) (D)  int_(0)^(80)r(x)dx

Bytelearn · Accepted Answer

Calculate Change in Revenue: To find the total expected revenue when the ticket price is $80, we need to calculate the change in revenue from when the ticket price was $70 to when it is $80. The rate of change of the revenue function, r(x), is given as a function of the ticket price x. To find the change in revenue, we integrate the rate of change from the initial price to the final price.Use Integral of Rate of Change: The correct expression to use for this calculation is the integral of the rate of change function, r(x), from the initial price of $70 to the final price of $80. This is because the integral of a rate of change function gives us the total change in the function over the interval.Expression for Total Change: The expression that represents the total change in revenue from a ticket price of $70 to $80 is the integral of r(x) from 70 to 80. This is represented by the expression $ 128 + \int_{70}^{80} r(x) \, dx $. This means we add the change in revenue to the initial revenue of 128 thousand dollars.Calculate Integral of r(x): Now we need to calculate the integral of r(x) from 70 to 80. The function r(x) is given by $ r(x) = 17 - 0.24x $. We integrate this function from 70 to 80.Evaluate Antiderivative at Limits: The integral of $ r(x) = 17 - 0.24x $ from 70 to 80 is calculated as follows: $$ \int_{70}^{80} (17 - 0.24x) \, dx = [17x - 0.12x^2]_{70}^{80} $$Perform Calculations: We evaluate the antiderivative at the upper and lower limits of the integral: $$ [17(80) - 0.12(80)^2] - [17(70) - 0.12(70)^2] $$Simplify Calculations: Performing the calculations, we get: $$ [1360 - 0.12(6400)] - [1190 - 0.12(4900)] $$Find Change in Revenue: Simplifying the calculations, we find: $$ [1360 - 768] - [1190 - 588] $$Identify Mistake: Further simplifying, we get: $$ [592] - [602] $$Recalculate Change: Subtracting the two values, we find a change in revenue of: $$ 592 - 602 = -10 $$ This result indicates a decrease in revenue of 10 thousand dollars when the ticket price increases from $70 to $80.However, this result does not make sense because the integral should give us a positive change in revenue since we are adding to the initial revenue. There must be a mistake in the calculation. Let's recheck the calculations.

Full solution

More problems from Solve one-step multiplication and division equations: word problems

Related topics