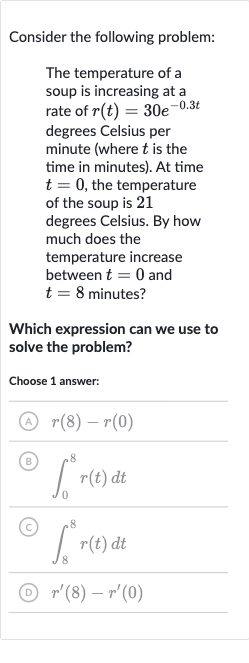
Consider the following problem: The temperature of a soup is increasing at a rate of r(t)=30e^(-0.3 t) degrees Celsius per minute (where t is the time in minutes). At time t=0, the temperature of the soup is 21 degrees Celsius. By how much does the temperature increase between t=0 and t=8 minutes? Which expression can we use to solve the problem? Choose 1 answer: (A) r(8)-r(0) (B) int_(0)^(8)r(t)dt (C) int_(8)^(8)r(t)dt (D) r^(')(8)-r^(')(0)

Question

Consider the following problem: The temperature of a soup is increasing at a rate of  r(t)=30e^(-0.3 t) degrees Celsius per minute (where  t is the time in minutes). At time  t=0, the temperature of the soup is 21 degrees Celsius. By how much does the temperature increase between  t=0 and  t=8 minutes? Which expression can we use to solve the problem? Choose 1 answer: (A)  r(8)-r(0) (B)  int_(0)^(8)r(t)dt (C)  int_(8)^(8)r(t)dt (D)  r^(')(8)-r^(')(0)

Bytelearn · Accepted Answer

Rate of Temperature Change Function: To find the total increase in temperature over a period of time, we need to integrate the rate of temperature change over that time interval. The rate of temperature change is given by the function r(t) = 30e^(-0.3t). We are interested in the interval from t=0 to t=8 minutes.Calculate Total Increase: The correct expression to calculate the total increase in temperature from t=0 to t=8 is the integral of r(t) from 0 to 8. This is because integration will give us the total accumulation of the temperature change over the time interval.Mathematical Representation: The integral of r(t) from 0 to 8 is represented mathematically as ∫(from 0 to 8) r(t) dt. This corresponds to choice (B) int_(0)^(8)r(t)dt.Calculate Integral: We can now calculate the integral to find the total temperature increase. The integral of 30e^(-0.3t) from 0 to 8 is: ∫(from 0 to 8) 30e^(-0.3t) dt = [-100e^(-0.3t)] (from 0 to 8)Evaluate Integral: Evaluating the integral at the bounds gives us: -100e^(-0.3*8) - (-100e^(-0.3*0)) = -100e^(-2.4) - (-100e^(0))Simplify Expression: Simplifying the expression gives us: -100/e^(2.4) - (-100) = 100 - 100/e^(2.4)Calculate Value of e^(2.4): Using a calculator to find the value of e^(2.4), we get approximately: 100 - 100/11.02317638 ≈ 100 - 9.076923Subtract Values: Subtracting the two values gives us the total temperature increase: 100 - 9.076923 ≈ 90.923077

Full solution

More problems from Solve one-step multiplication and division equations: word problems

Related topics