AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
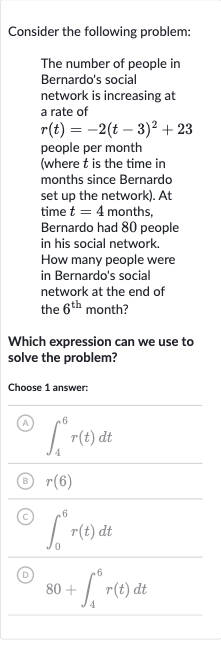
Consider the following problem:The number of people in Bernardo's social network is increasing at a rate of people per month (where is the time in months since Bernardo set up the network). At time months, Bernardo had people in his social network. How many people were in Bernardo's social network at the end of the month?Which expression can we use to solve the problem?Choose answer:(A) (B) (C) (D)
Full solution
Q. Consider the following problem:The number of people in Bernardo's social network is increasing at a rate of people per month (where is the time in months since Bernardo set up the network). At time months, Bernardo had people in his social network. How many people were in Bernardo's social network at the end of the month?Which expression can we use to solve the problem?Choose answer:(A) (B) (C) (D)
- Calculate Change in People: To find the number of people in Bernardo's social network at the end of the month, we need to calculate the change in the number of people from the month to the month and add it to the number of people he had at the month. The rate of change of the number of people in his network is given by the function . We need to integrate this rate function from to to find the total change in the number of people during this time period.
- Rate Function Integration: The correct expression to calculate the total change in the number of people from the month to the month is the definite integral of from to . This is because integration of the rate function over a time interval gives us the net change in the quantity over that interval.
- Total Change Calculation: The expression that represents the total change in the number of people from the month to the month is therefore . This corresponds to choice (A) .
- Final Number of People Calculation: To find the total number of people in the network at the end of the month, we need to add the result of the integral to the number of people Bernardo had at the month, which is . So the correct expression to find the total number of people at the end of the month is . This corresponds to choice (D) .
