Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Consider the equation
0.75*10^((w)/(3))=30
Solve the equation for
w. Express the solution as a logarithm in base-10.

w=

◻
Approximate the value of
w. Round your answer to the nearest thousandth.

w~~

Consider the equation $\newline$ $0.75\times10^{\left(\frac{w}{3}\right)}=30$ $\newline$ Solve the equation for $\newline$ $w$ . Express the solution as a logarithm in base $-10$ . $\newline$ $w=$ $\newline$ $\square$ $\newline$ Approximate the value of $\newline$ $w$ . Round your answer to the nearest thousandth. $\newline$ $w\approx$

View step-by-step help

View step-by-step help

Find the roots of factored polynomials

Full solution

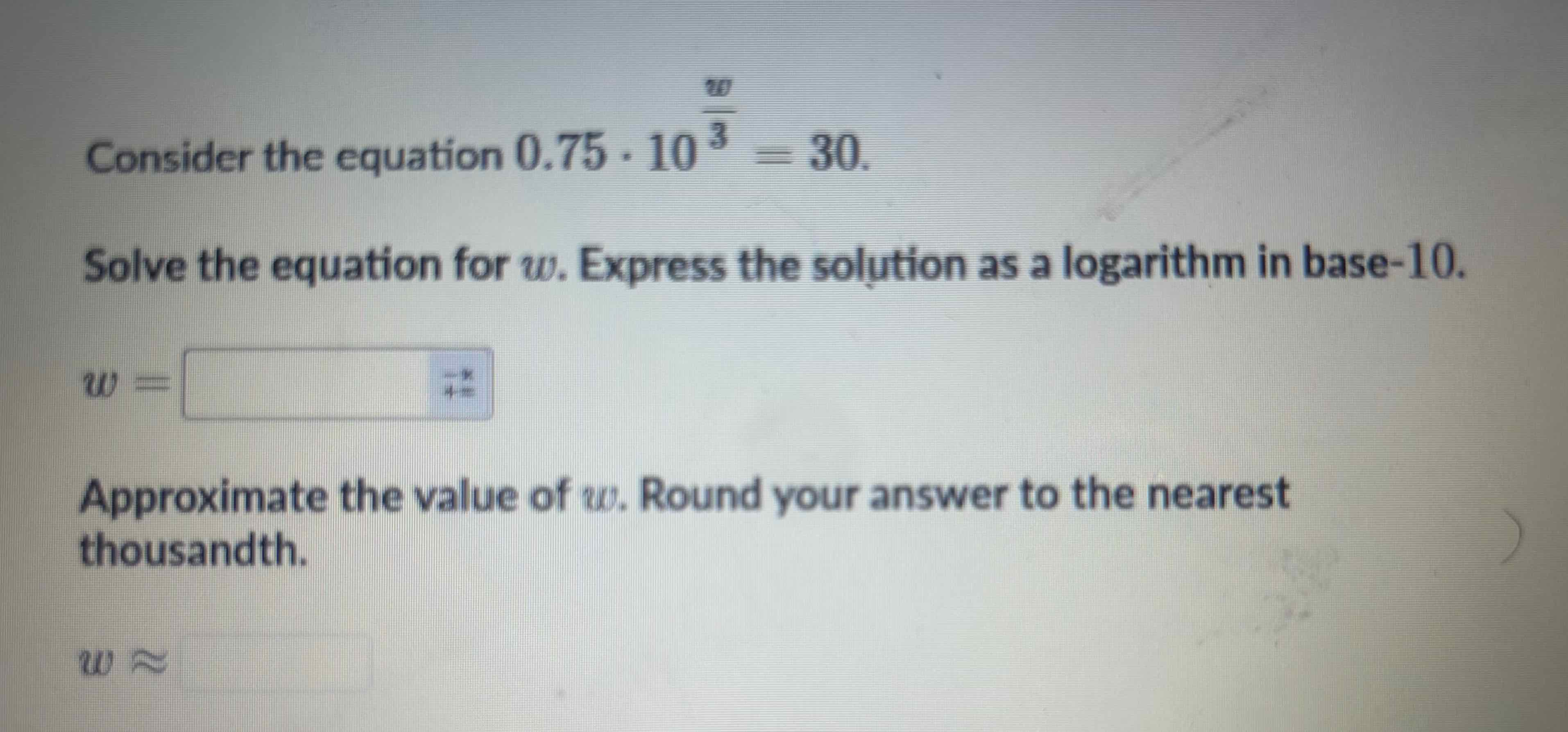
Q. Consider the equation

\newline

0.75\times10^{\left(\frac{w}{3}\right)}=30

\newline

Solve the equation for

\newline

w

. Express the solution as a logarithm in base

-10

.

\newline

w=

\newline

\square

\newline

Approximate the value of

\newline

w

. Round your answer to the nearest thousandth.

\newline

w\approx

Isolate $10^{w/3}$ : Isolate $10^{w/3}$ by dividing both sides by $0.75$ : $0.75\cdot10^{w/3} = 30 \rightarrow 10^{w/3} = \frac{30}{0.75} = 40.$
Apply logarithm base $-10$ : Apply logarithm base $-10$ to both sides to solve for $w/3$ : $\log_{10}(10^{w/3}) = \log_{10}(40)$ .
Simplify using logarithm property: Simplify using the property of logarithms $\log_b(b^x) = x$ : $\frac{w}{3} = \log_{10}(40)$ .
Solve for w: Solve for w by multiplying both sides by $3$ : $w = 3 \times \log_{10}(40)$ .
Approximate $\log_{10}(40)$ : Use a calculator to approximate $\log_{10}(40)$ : $\log_{10}(40) \approx 1.602$ .
Calculate w: Calculate $w$ : $w \approx 3 \times 1.602 = 4.806$ .

More problems from Find the roots of factored polynomials

Question

Find the solutions of the quadratic equation

2 x^{2}-8 x-9=0

\newline

1

\newline

2 \pm \frac{\sqrt{34}}{2} i

\newline

-2 \pm \frac{\sqrt{34}}{2} i

\newline

2 \pm \frac{\sqrt{34}}{2}

\newline

1 \pm \frac{\sqrt{34}}{4}

Posted 3 months ago

Question

x^{3}+7 x^{2}-36

\newline

The polynomial has zeros at

-6

2

. If the remaining zero is

z

, then what is the value of

-z

Posted 3 months ago

Question

x

\newline

Enter the solutions from least to greatest.

\newline

\begin{array}{l} (-5 x+4)(x-3)=0 \\ \text { lesser } x=\square \\ \text { greater } x=\square \end{array}

Posted 3 months ago

Question

x

\newline

Enter the solutions from least to greatest.

\newline

(2 x+4)(3 x-2)=0

\newline

x=

\newline

x=

Posted 3 months ago

Question

x

\newline

Enter the solutions from least to greatest.

\newline

\begin{array}{l} (3 x-6)(-x+3)=0 \\ \text { lesser } x=\square \\ \text { greater } x=\square \end{array}

Posted 3 months ago

Question

x

\newline

Enter the solutions from least to greatest.

\newline

(x+6)(-x+1)=0

\newline

x=

\newline

x=

Posted 3 months ago

Question

Is the following function even, odd, or neither?

\newline

f(x)=\frac{3}{x^{2}+2}

\newline

1

\newline

\newline

\newline

Posted 3 months ago

Question

Is the following function even, odd, or neither?

\newline

f(x)=\frac{1}{4-x^{2}}

\newline

1

\newline

\newline

\newline

Posted 3 months ago

Question

Is the following function even, odd, or neither?

\newline

f(x)=2|x|-5

\newline

1

\newline

\newline

\newline

Posted 3 months ago

Question

Is the following function even, odd, or neither?

\newline

f(x)=\frac{x}{x^{2}+1}

\newline

1

\newline

\newline

\newline

Posted 3 months ago