Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Condense the logarithm

log d-7log k
Answer:
log(◻)

Condense the logarithm $\newline$ $\log d-7 \log k$ $\newline$ Answer: $\log (\square)$

View step-by-step help

View step-by-step help

Convert between exponential and logarithmic form

Full solution

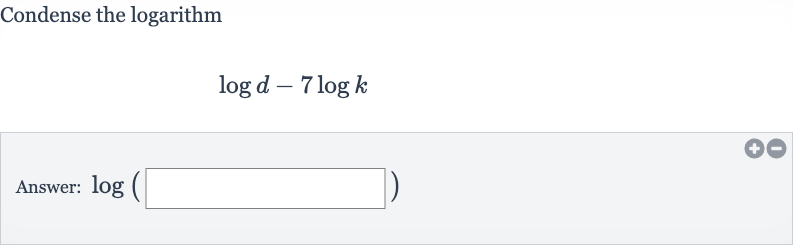
Q. Condense the logarithm

\newline

\log d-7 \log k

\newline

Answer:

\log (\square)

Rewrite second term: We are given the expression $\log(d) - 7\log(k)$ and we need to condense it into a single logarithm. $\newline$ According to the logarithm power rule, $\log_b(a^n) = n\log_b(a)$ , we can rewrite the second term as a logarithm of a power. $\newline$ $\log(d) - 7\log(k) = \log(d) - \log(k^7)$
Combine logarithms: Now, we can use the logarithm subtraction rule, which states that $\log_b(a) - \log_b(c) = \log_b(\frac{a}{c})$ , to combine the two logarithms into one. $\newline$ $\log(d) - \log(k^7) = \log(\frac{d}{k^7})$

More problems from Convert between exponential and logarithmic form

Question

x

\newline

5^x=1

\newline

\newline

Write your answer in simplest form.

Posted 5 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

Posted 4 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

Posted 5 months ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 8 months ago

Question

x

\newline

7 = 9^x

\newline

Round your answer to the nearest thousandth.

Posted 4 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 7 months ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 9 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 7 months ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 4 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6x

\newline

f(x) = 6^x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 4 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant