Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Condense the logarithm log d+2log q Answer: log(◻)

Condense the logarithm\newlinelog⁡d+2log⁡q \log d+2 \log q \newlineAnswer: log⁡(□) \log (\square)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Convert between exponential and logarithmic formright chevron icon

Full solution

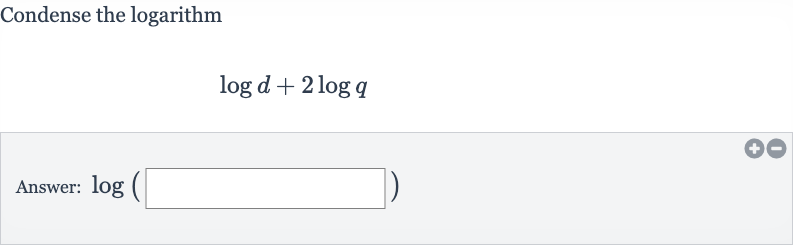
Q. Condense the logarithm\newlinelog⁡d+2log⁡q \log d+2 \log q \newlineAnswer: log⁡(□) \log (\square)
  1. Apply Logarithm Power Rule: We are given the expression log⁡d+2log⁡q\log d + 2\log q and we need to condense it into a single logarithm.\newlineAccording to the logarithm power rule, which states that alog⁡b=log⁡(ba)a\log b = \log(b^a), we can rewrite 2log⁡q2\log q as log⁡(q2)\log(q^2).
  2. Apply Logarithm Product Rule: Now we have log⁡d+log⁡(q2)\log d + \log(q^2). According to the logarithm product rule, which states that log⁡a+log⁡b=log⁡(ab)\log a + \log b = \log(ab), we can combine these two logarithms into one.\newlineSo, log⁡d+log⁡(q2)\log d + \log(q^2) becomes log⁡(d⋅q2)\log(d \cdot q^2).
  3. Final Condensed Form: We have successfully condensed the logarithm expression into a single logarithm without any mathematical errors.\newlineThe final condensed form is log⁡(d⋅q2)\log(d \cdot q^{2}).

More problems from Convert between exponential and logarithmic form

Question
Solve. Write your answer as an integer or a fraction in simplest form.\newline5x=15^x=1\newlinex=x= _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Steven opened a savings account and deposited $100.00\$100.00 as principal. The account earns 9%9\% interest, compounded annually. What is the balance after 55 years?\newlineUse the formula A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}, where AA is the balance (final amount), PP is the principal (starting amount), rr is the interest rate expressed as a decimal, nn is the number of times per year that the interest is compounded, and tt is the time in years.\newlineRound your answer to the nearest cent.\newline$\$____
Get tutor helpright-arrow

Posted 2 months ago

Question
Use the following function rule to find f(1) f(1) .\newlinef(x)=12(7)x+8 f(x) = 12(7)^x + 8 \newlinef(1)= f(1) = _____
Get tutor helpright-arrow

Posted 1 month ago

Question
The town of Valley View conducted a census this year, which showed that it has a population of 1,8001,800 people. Based on the census data, it is estimated that the population of Valley View will grow by 12%12\% each decade.\newlineWrite an exponential equation in the form y=a(b)xy = a(b)^x that can model the town population, yy, xx decades after this census was taken.\newlineUse whole numbers, decimals, or simplified fractions for the values of aa and bb.\newliney=y = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Round your answer to the nearest thousandth.\newline7=9x7 = 9^x\newlinex=x = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Round your answer to the nearest thousandth.\newline7=ex7 = e^x\newlinex=x = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve. Simplify your answer.\newlinelog⁡u=1\log u = 1\newlineu=u = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Simplify your answer.\newline7log⁡x=77\log x = 7\newlinex=x = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
How does g(t)=3t g(t) = 3^t change over the interval from t=3 t = 3 to t=4 t = 4 ?\newlineChoices:\newline(A) g(t) g(t) decreases by 3 3 \newline(B) g(t) g(t) increases by 3 3 \newline(C) g(t) g(t) decreases by 3% 3\%\newline(D) g(t) g(t) increases by 200%200\%
Get tutor helpright-arrow

Posted 2 months ago

Question
A function f(x) f(x) increases by 6 6 over every unit interval in x x and f(0)=0 f(0) = 0 .\newlineWhich could be a function rule for f(x) f(x) ?\newlineChoices:\newline(A) f(x)=6xf(x) = 6^x\newline(B) f(x)=6xf(x) = 6x\newline(C) f(x)=16xf(x) = \frac{1}{6^x}\newline(D) f(x)=x6f(x) = \frac{x}{6}
Get tutor helpright-arrow

Posted 2 months ago

View all (49)