AI tutor
Full solution
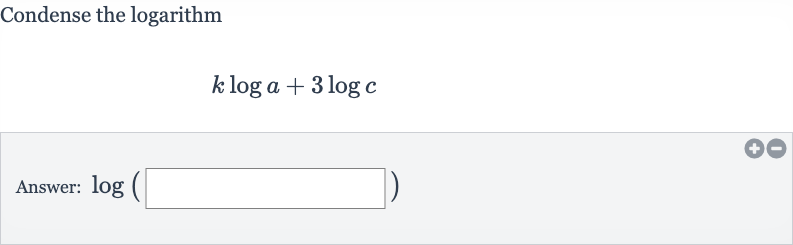
Q. Condense the logarithmAnswer:
- Identify Properties: Identify the properties used to condense the logarithm. The properties used to condense the logarithm are the power rule and the product rule for logarithms. The power rule states that , and the product rule states that .
- Apply Power Rule: Apply the power rule to each term.Using the power rule, we can rewrite as and as .
- Apply Product Rule: Apply the product rule to combine the logarithms.Using the product rule, we can combine and into a single logarithm: .
- Write Final Expression: Write the final condensed logarithmic expression.The final condensed logarithmic expression is .
More problems from Quotient property of logarithms
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help