Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Condense the logarithm

g log a+log d
Answer:
log(◻)

Condense the logarithm $\newline$ $g \log a+\log d$ $\newline$ Answer: $\log (\square)$

View step-by-step help

View step-by-step help

Convert between exponential and logarithmic form

Full solution

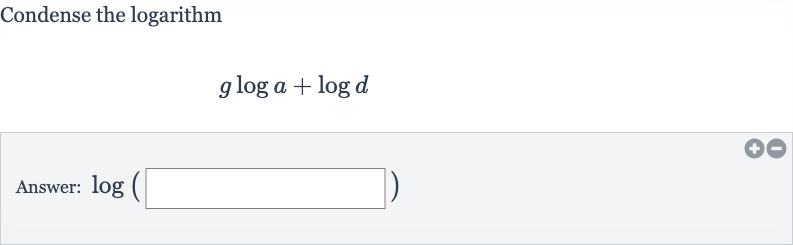
Q. Condense the logarithm

\newline

g \log a+\log d

\newline

Answer:

\log (\square)

Question Prompt: Question prompt: Condense the expression $g \log a + \log d$ into a single logarithm.
Combine Logarithms: Apply the logarithm property that allows us to combine two logarithms with the same base that are being added into a single logarithm by multiplying their arguments. $\newline$ The property is $\log_b(m) + \log_b(n) = \log_b(m*n)$ , where $b$ is the base of the logarithms.
Rewrite Coefficient: Use the property from Step $1$ to combine $g \log a + \log d$ . Since $g$ is a coefficient of $\log a$ , we can rewrite it as $\log a^g$ using the property that $g\log_b(m) = \log_b(m^g)$ . So, $g \log a + \log d = \log a^g + \log d$ .
Final Simplification: Now apply the property from Step $1$ to the expression $\log a^g + \log d$ . This gives us $\log(a^g \cdot d)$ .

More problems from Convert between exponential and logarithmic form

Question

Solve. Write your answer as an integer or a fraction in simplest form.

\newline

5^x=1

\newline

x=

Posted 2 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

Posted 2 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

\newline

f(1) =

Posted 1 month ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = 9^x

\newline

x =

Posted 2 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 1 month ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 2 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 1 month ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 2 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6^x

\newline

f(x) = 6x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 2 months ago