Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Condense the logarithm 5log b+3log r Answer: log(◻)

Condense the logarithm\newline5log⁡b+3log⁡r 5 \log b+3 \log r \newlineAnswer: log⁡(□) \log (\square)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Quotient property of logarithmsright chevron icon

Full solution

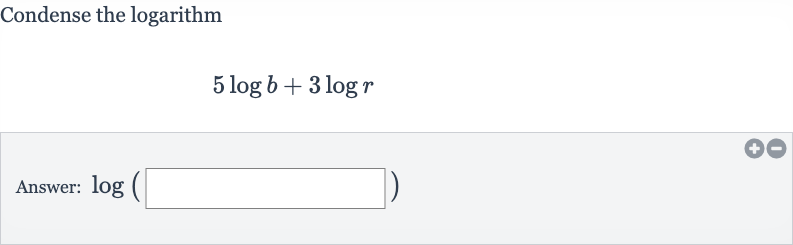
Q. Condense the logarithm\newline5log⁡b+3log⁡r 5 \log b+3 \log r \newlineAnswer: log⁡(□) \log (\square)
  1. Identify Property: Identify the property used to condense the logarithm.\newlineWhen you have a coefficient in front of a logarithm, you can use the power property to move the coefficient inside the logarithm as an exponent of the argument.\newlinePower Property: n⋅log⁡b(P)=log⁡b(Pn)n \cdot \log_b (P) = \log_b (P^n)
  2. Apply Power Property: Apply the power property to each term.\newlineFor the first term, 5log⁡b5\log b, we apply the power property to get log⁡(b5)\log(b^5).\newlineFor the second term, 3log⁡r3\log r, we apply the power property to get log⁡(r3)\log(r^3).
  3. Combine Using Product Property: Combine the two logarithms into one using the product property.\newlineProduct Property: log⁡bP+log⁡bQ=log⁡b(P×Q)\log_b P + \log_b Q = \log_b (P \times Q)\newlineCombine log⁡(b5)\log(b^5) and log⁡(r3)\log(r^3) using the product property to get log⁡(b5×r3)\log(b^5 \times r^3).

More problems from Quotient property of logarithms

Question
Write the exponential equation in logarithmic form.\newline93=7299^3 = 729\newlinelog⁡□729=3\log_\square 729 = 3
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the exponential equation in logarithmic form.\newlinee4≈54.598e^4 \approx 54.598\newlineln⁡____≈4\ln\_\_\_\_ \approx 4
Get tutor helpright-arrow

Posted 2 months ago

Question
Write the logarithmic equation in exponential form.\newlinelog⁡10100=2\log_{10}100 = 2\newline102=‾10^2 = \underline{\hspace{2em}}
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer as a whole number, proper fraction, or improper fraction in simplest form.\newlineln⁡(e)10=\frac{\ln (e)}{10} = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Rewrite as a quotient of two common logarithms. Write your answer in simplest form.\newlinelog⁡333=\log_3 33 = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Round your answer to the nearest thousandth.\newlinelog⁡550=\log_{5}50 = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Which property of logarithms does this equation demonstrate? \newlinelog⁡33+log⁡36=log⁡318\log_3 3 + \log_3 6 = \log_3 18\newlineChoices:\newline(A) Product Property\text{Product Property}\newline(B) Power Property\text{Power Property}\newline(C) Quotient Property\text{Quotient Property}
Get tutor helpright-arrow

Posted 2 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡(uv)\log(uv)\newline_____
Get tutor helpright-arrow

Posted 2 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of common logarithms or multiples of common logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡v7\log v^7 \newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Expand the logarithm. Assume all expressions exist and are well-defined.\newlineWrite your answer as a sum or difference of base-66 logarithms or multiples of base-66 logarithms. The inside of each logarithm must be a distinct constant or variable.\newlinelog⁡6w6\log_6 w^6\newline______
Get tutor helpright-arrow

Posted 2 months ago

View all (60)