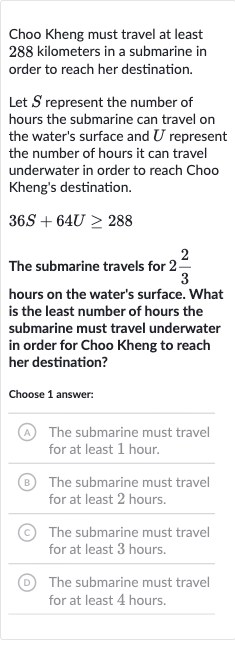
Choo Kheng must travel at least 288 kilometers in a submarine in order to reach her destination. Let S represent the number of hours the submarine can travel on the water's surface and U represent the number of hours it can travel underwater in order to reach Choo Kheng's destination. 36 S+64 U = 288 The submarine travels for 2(2)/(3) hours on the water's surface. What is the least number of hours the submarine must travel underwater in order for Choo Kheng to reach her destination? Choose 1 answer: (A) The submarine must travel for at least 1 hour. (B) The submarine must travel for at least 2 hours. (C) The submarine must travel for at least 3 hours. (D) The submarine must travel for at least 4 hours.

Question

Choo Kheng must travel at least 288 kilometers in a submarine in order to reach her destination. Let  S represent the number of hours the submarine can travel on the water's surface and  U represent the number of hours it can travel underwater in order to reach Choo Kheng's destination.  36 S+64 U >= 288 The submarine travels for  2(2)/(3) hours on the water's surface. What is the least number of hours the submarine must travel underwater in order for Choo Kheng to reach her destination? Choose 1 answer: (A) The submarine must travel for at least 1 hour. (B) The submarine must travel for at least 2 hours. (C) The submarine must travel for at least 3 hours. (D) The submarine must travel for at least 4 hours.

Bytelearn · Accepted Answer

Substitute Time on Surface: Substitute the given time on the water's surface into the equation. The submarine travels for $ \frac{2}{3} \times 2 $ hours on the water's surface, which is $ \frac{4}{3} $ hours or approximately 1.33 hours. We substitute this value into the equation for S. $ 36S + 64U \geq 288 $ $ 36 \times \frac{4}{3} + 64U \geq 288 $Calculate Distance on Surface: Perform the multiplication to find the distance covered on the water's surface. $ 36 \times \frac{4}{3} = 48 $ So, the distance covered on the water's surface is 48 kilometers. $ 48 + 64U \geq 288 $Subtract Distance Covered: Subtract the distance covered on the water's surface from the total distance required. $ 64U \geq 288 - 48 $ $ 64U \geq 240 $Divide to Solve for U: Divide both sides by 64 to solve for U. $ U \geq \frac{240}{64} $ $ U \geq 3.75 $Round Up to Next Hour: Since U must be an integer number of hours and the submarine must travel at least 3.75 hours underwater, we round up to the next whole hour. The submarine must travel for at least 4 hours underwater.

Full solution

More problems from One-step inequalities: word problems

Related topics