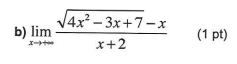Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

b)
lim_(x rarr+oo)(sqrt(4x^(2)-3x+7)-x)/(x+2)

(1pt)

$\lim _{x \rightarrow+\infty} \frac{\sqrt{4 x^{2}-3 x+7}-x}{x+2}$ $\newline$

View step-by-step help

View step-by-step help

Add and subtract polynomials

Full solution

Q.

\lim _{x \rightarrow+\infty} \frac{\sqrt{4 x^{2}-3 x+7}-x}{x+2}

\newline

Simplify Inside Square Root: Simplify the expression inside the square root for large $x$ values. $\newline$ As $x$ approaches infinity, the term $-3x$ becomes negligible compared to $4x^2$ , so we approximate $\sqrt{4x^2 - 3x + 7} \approx \sqrt{4x^2}$ .
Simplify Square Root: Simplify the square root. $\sqrt{4x^2} = 2x$ , because the square root and square cancel out, and we take the positive root since $x$ is approaching infinity.
Substitute Back: Substitute back into the original limit expression. $\newline$ Replace $\sqrt{4x^2 - 3x + 7}$ with $2x$ in the limit expression: $\frac{2x - x}{x + 2}$ .
Simplify Numerator: Simplify the numerator. $2x - x = x$ .
Simplify Entire Expression: Simplify the entire expression. $\newline$ $\frac{x}{x + 2} = \frac{1}{1 + \frac{2}{x}}$ .
Evaluate Limit: Evaluate the limit as $x$ approaches infinity. $\newline$ As $x$ approaches infinity, $\frac{2}{x}$ approaches $0$ , so $1 + \frac{2}{x}$ approaches $1$ . Therefore, the limit of $\frac{1}{1 + \frac{2}{x}}$ as $x$ approaches infinity is $1$ .

More problems from Add and subtract polynomials

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 2 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 1 month ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 2 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 2 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 2 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 2 months ago