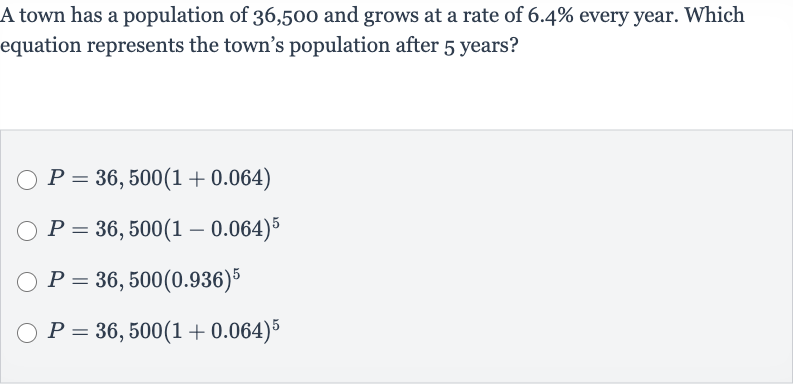Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A town has a population of 36,500 and grows at a rate of
6.4% every year. Which equation represents the town's population after 5 years?

P=36,500(1+0.064)

P=36,500(1-0.064)^(5)

P=36,500(0.936)^(5)

P=36,500(1+0.064)^(5)

A town has a population of $36$ , $500$ and grows at a rate of $6.4 \%$ every year. Which equation represents the town's population after $5$ years? $\newline$ $P=36,500(1+0.064)$ $\newline$ $P=36,500(1-0.064)^{5}$ $\newline$ $P=36,500(0.936)^{5}$ $\newline$ $P=36,500(1+0.064)^{5}$

View step-by-step help

View step-by-step help

Write exponential functions: word problems

Full solution

Q. A town has a population of

36

,

500

and grows at a rate of

6.4 \%

every year. Which equation represents the town's population after

5

years?

\newline

P=36,500(1+0.064)

\newline

P=36,500(1-0.064)^{5}

\newline

P=36,500(0.936)^{5}

\newline

P=36,500(1+0.064)^{5}

Rephrase the Question: First, let's rephrase the ＂What is the equation that represents the town's population after $5$ years, given an initial population of $36,500$ and an annual growth rate of $6.4\%$ ?＂
Identify Initial Population and Growth Rate: Identify the initial population $P_0$ and the growth rate $r$ . The initial population is given as $36,500$ , and the growth rate is $6.4\%$ , which can be expressed as a decimal by dividing by $100$ : $r = \frac{6.4}{100} = 0.064$ .
Determine Growth Factor: Determine the growth factor $b$ . The growth factor is $1$ plus the growth rate, so $b = 1 + r = 1 + 0.064 = 1.064$ .
Write Exponential Growth Equation: Write the exponential growth equation. The general form of an exponential growth equation is $P = P_0 \times b^t$ , where $P$ is the population after time $t$ , $P_0$ is the initial population, $b$ is the growth factor, and $t$ is the time in years. In this case, $t = 5$ years.
Substitute Known Values: Substitute the known values into the equation to get the specific equation for this problem: $P = 36,500 \times (1.064)^5$ .

More problems from Write exponential functions: word problems

Question

Use the following function rule to find

f(2)

\newline

f(x) = 11 \cdot (9)^x + 8

\newline

f(2) =

Posted 2 months ago

Question

Raymond works for a pharmaceutical company that is testing the effectiveness of a new medication. He gave one of the study participants

400

milligrams of the medication, and he knows the amount remaining in the participant's body will decrease by a factor of

1/3

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the amount of medication,

y

, remaining in the participant's body after

x

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

\newline

Posted 2 months ago

Question

100

bacteria doubles in size every

60

hours. What will the population be

180

hours from now?

\newline

Posted 2 months ago

Question

Charlotte opened a savings account and deposited

\$800.00

as principal. The account earns

8\%

interest, compounded annually. What is the balance after

10

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

\newline

\$

\newline

Posted 2 months ago

Question

Bob rented a car for a flat fee of `$150` and an additional `$10` per day. Write a linear function that represents the total cost,

f(x)

x

Posted 3 months ago

Question

Sally purchased a laptop for `$800` and has to pay a service fee of `$20` for each day until it is delivered. Write a linear function to represent the total cost,

h(x)

x

Posted 3 months ago

Question

\$1,000

in a savings account with a daily interest rate of

0.1\%

. Write an exponential function to represent the total amount,

s(x)

, in his account after

x

Posted 3 months ago

Question

A=2450+740 s

\newline

The total amount,

A

, in thousands of dollars, of scholarship money given out by a college throughout its history at a time of

s

semesters after the summer of the year

2000

is given by the equation. What was the total amount of scholarship money, in thousands of dollars, given out by the college up to the summer of the year

2000

Posted 1 month ago

Question

T=235+980 d

\newline

T

, in newton-meters, on a diving board with a

100

kilogram weight placed

d

meters from the diving board's fulcrum is given by the equation. How much torque in newton-meters is on the diving board when the weight is placed at the fulcrum?

Posted 2 months ago

Question

R=42-0.7 t

\newline

Quinn returned home one summer's day to find it extremely hot. He turned the air conditioner on, and the room's temperature began decreasing at a constant rate. The given equation shown gives the room's temperature,

R

, in degrees Celsius,

t

minutes after Quinn turned on the air conditioner. What was the room's temperature, in degrees Celsius, when Quinn returned home?

Posted 1 month ago